20 câu trắc nghiệm Toán 8 Cánh diều Ôn tập chương III (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong các hàm số sau, hàm số nào không là hàm số bậc nhất?
\(y = 4 - x.\)
\(y = \frac{{1 + 2x}}{2}.\)
\(y = {x^2} + x.\)
\(y = \frac{1}{2}x - 3.\)
Cho hình vẽ bên. Đường thẳng \[OA\] là đồ thị của hàm số
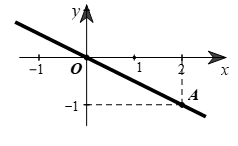
\[y = -2x.\]
\[y = -0,5x.\]
\(y = \frac{1}{2}x.\)
\[y = 2x.\]
Đường thẳng có hệ số góc bằng \[-4\]và đi qua điểm \[A\left( {3;-2} \right)\] là
\[y = -4x + 10.\]
\[y = 4x + 10.\]
\[y = -4x-10.\]
\[y = -4x.\]
Trong các điểm sau, điểm nào thuộc đồ thị hàm số \(y = - \frac{1}{2}x + 1?\)
\(\left( {1;\frac{1}{2}} \right).\)
\(\left( {3;3} \right).\)
\(\left( { - 1;\frac{1}{2}} \right).\)
\(\left( { - 2; - 1} \right).\)
Đường thẳng \[y = 1-3x\] có hệ số góc là
\( - 3.\)
\( - 1.\)
\(1.\)
\(3.\)
Hai đường thẳng \(y = \left( {m - 1} \right)x + 2\,\,\left( {m \ne 1} \right)\) và \(y = 3x + 2\) trùng nhau khi
\(m = - 4.\)
\(m = - 2.\)
\(m = 4.\)
\(m \ne - 4.\)
Nếu hai đường thẳng \[y = -3x + 4\]và \[y = \left( {m + 2} \right)x + m\] song song với nhau thì giá trị của \[m\] bằng
\[-5.\]
\[-3.\]
\[-2.\]
\[3.\]
Góc tạo bởi đường thẳng \(y = 5 - 4x\) với trục \[Ox\] là
góc nhọn.
góc vuông.
góc tù.
góc bẹt.
Cho hai hàm số \[y = \left( {m + 3} \right)x-m\]và \[y = 3x-3m + 2.\] Giá trị của \[m\] để đồ thị của hai hàm số trên vuông góc với nhau là
\[\frac{{10}}{3}.\]
\[-\frac{{10}}{3}.\]
\(\frac{8}{3}.\)
\( - \frac{8}{3}.\)
Hai đường thẳng \[y = x + 2\] và \[y = 2x + 2\] trên cùng một mặt phẳng tọa độ có vị trí tương đối là
Trùng nhau.
Cắt nhau tại điểm có tung độ là 2.
Song song với nhau.
Cắt nhau tại điểm có tung độ là \[-2.\]
Cho hai đường thẳng \(\left( {{d_1}} \right):y = 2x + 1,\)\(\left( {{d_2}} \right):y = x + 1\).
Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cắt nhau.
Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right).\)
Đường thẳng \(\left( {{d_3}} \right)\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\) là \(y = 2x - 1.\)
Đường thẳng \(\left( {{d_4}} \right)\) đi qua \(A\), cắt đường thẳng \(\left( {{d_2}} \right)\) và có hệ số góc là \(3\) là đường thẳng \(y = 3x + 1.\)
Cho hai đường thẳng \(\left( d \right):y = 4x + m\) và \(\left( {d'} \right):y = - 3x + 2 - m\).
Hai đường thẳng luôn cắt nhau với mọi giá trị của \(m.\)
Với \(m = - 4\) thì chỉ đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1;0} \right)\).
Với \(m = 4\) thì hai đường thẳng cắt nhau tại điểm \(\left( {\frac{6}{7};\frac{4}{7}} \right).\)
Điều kiện của \(m\) để hai đường thẳng \(\left( d \right),\left( {d'} \right)\) cắt nhau tại 1 điểm nằm bên phải trục tung là \(m < 1.\)
Cho hàm số \(\left( d \right):y = \left( {2 - m} \right)x + 3m - 1\).
Điều kiện để hàm số trên là hàm bậc nhất là \(m = 2.\)
Với \(m = - 1\) thì đồ thị hàm số \(\left( d \right)\) đi qua điểm \(A\left( {0;4} \right).\)
Để \(\left( d \right)\) song song với \(\left( {d'} \right):y = - x + m - 3\) thì \(m = 3.\)
Để \(\left( d \right)\) cắt đường thẳng \(\left( {d''} \right):y = - x + 2\) tại một điểm thuộc trục tung thì \(m = 1.\)
Cho ba đường thẳng \(\left( {{d_1}} \right):y = - 2x,\)\(\left( {{d_2}} \right):y = 1,5x + 7\) và \(\left( {{d_3}} \right):y = - 2mx + 5.\)
Hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng \( - 2.\)
\(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( { - 2;4} \right).\)
Để \(\left( {{d_3}} \right)\) cắt \(\left( {{d_1}} \right)\) thì \(m \ne - \frac{3}{4}.\)
ba đường thẳng \(\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right)\) cắt nhau tại một điểm thì \(m = \frac{1}{4}.\)
Cho hàm số \(\left( d \right):y = 2x + 4\) và \(\left( {d'} \right):y = \left( {m - 2} \right)x + m + 2.\)
Với \(m = 0\) thì hai đường thẳng cắt nhau.
Với \(m = 2\) thì hai đường thẳng song song.
Khi \(m = 0\) thì hai đường thẳng cùng đi qua điểm \(M\left( {\frac{1}{2};3} \right).\)
Để hai đường thẳng cắt nhau tại một điểm thuộc trục hoành thì \(m = 6.\)
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\).
Cho hàm số \[f\left( x \right) = - \left| {2 - \frac{1}{2}x} \right|.\] Giá trị \[f\left( {-2} \right)\] bằng bao nhiêu?
Biết đường thẳng \(d:y = \left( {m + 2} \right)x - 5\) đi qua điểm \(A\left( { - 1;2} \right).\) Hỏi hệ số góc của đường thẳng đó bằng bao nhiêu?
Cho hàm số bậc nhất \[y = x + {m^2} + 1\] và \[y = 5 + \left( {m-1} \right)x.\]Giá trị của \[m\]để đồ thị hai hàm số cắt nhau tại một điểm trên trục tung là
Cho hai hàm số \[y = x + m + 1\] và \[y = 3 + \left( {m-1} \right)x.\]Với giá trị nào của \[m\]để đồ thị hai hàm số trên cắt nhau tại một điểm trên trục hoành?
