20 câu trắc nghiệm Toán 8 Cánh diều Bài 34. Trường hợp đồng dạng thứ hai của tam giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Nếu \(\Delta ABC\) và \(\Delta HIK\) có \(\frac{{AB}}{{HI}} = \frac{{AC}}{{HK}},\;\,\widehat A = \widehat H\) thì
\(\Delta ABC \sim \Delta HIK.\)
\(\Delta ABC \sim \Delta IHK.\)
\(\Delta ABC \sim \Delta HKI.\)
\(\Delta ABC \sim \Delta KHI.\)
Cho có \(\widehat A = 60^\circ ,\,\,\widehat E = 70^\circ \). Số đo của \(\widehat F\) là
\(60^\circ .\)
\(70^\circ .\)
\(80^\circ .\)
\(50^\circ .\)
Cho \(\Delta ABC\) vuông tại \(A,\;\Delta MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}.\) Khi đó:
\(\Delta ABC \sim \Delta MNP.\)
\(\Delta ABC \sim \Delta MPN.\)
\(\Delta ABC \sim \Delta NMP.\)
\(\Delta ABC \sim \Delta PMN.\)
Cho hình vẽ:
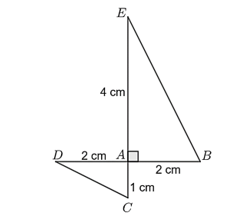
Khi đó:
\(\Delta ADC \sim \Delta ABE.\)
\(\Delta ACD \sim \Delta AEB.\)
\(\Delta ADC \sim \Delta AEB.\)
\(\Delta CDA \sim \Delta EBA.\)
Cho \(\Delta ABC\) vuông tại \(A.\) Lấy hai điểm \(M,\;\,N\) lần lượt thuộc các cạnh \(AB,\;\,AC\) sao cho \(AB = 3AN,\;\,BC = 3MN.\) Khi đó:
\(\widehat {AMN} = \widehat {ANM}.\)
\(\widehat {AMN} = \widehat C.\)
\(\widehat {AMN} = \widehat B.\)
\(\widehat {ANM} = \widehat C.\)
Cho \(\Delta ABC\) và \(\Delta DMN\) như hình vẽ dưới đây:

Để \(\Delta ABC \sim \Delta DMN\) (c.g.c) thì cần thêm yếu tố nào dưới đây?
\(\frac{{AB}}{{DM}} = \frac{{AC}}{{DN}}\).
\(\frac{{BC}}{{AC}} = \frac{{MN}}{{DN}}\).
\(\widehat B = \widehat M\).
Cả ba đáp án trên đều đúng.
Cho hình vẽ:

Biết rằng \(IK = 4\;{\rm{cm;}}\;\,KP = 3\;{\rm{cm}};\;\,CK = 1,5\;{\rm{cm}};\;\,KH = 2\;{\rm{cm}}.\) Khi đó:
\(\Delta KIH \sim \Delta KCP.\)
\(\Delta KIH \sim \Delta KPC.\)
\(\Delta IHK \sim \Delta PKC.\)
Cho hình vẽ:
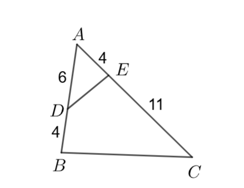
Biết rằng đơn vị đo trên các cạnh là mét, khi đó:
\(\widehat {ADE} = \frac{2}{3}\widehat C.\)
\(\widehat {ADE} = \frac{3}{4}\widehat C.\)
\(\widehat {ADE} = \widehat C.\)
\(\widehat C = \frac{3}{4}\widehat {ADE}.\)
\(\Delta ABC\) và \(\Delta DEF\) có \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\). Cần thêm yếu tố nào để hai tam giác này đồng dạng?
\(\widehat A = \widehat D\).
\(\widehat B = \widehat E\).
\(\widehat C = \widehat F\).
Cả A, B, C đều sai.
Cho \(\Delta ABC\), lấy hai điểm \(D,E\) lần lượt nằm trên hai cạnh \(AB,\,\,AC\) sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\). Kết luận nào sau đây là sai?
\(\Delta ABC \sim \Delta ADE\).
\(DE\parallel BC\).
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\).
\(\widehat {ADE} = \widehat {ABC}\).
Cho tam giác \(ABC\). Trên cạnh \(AB,AC\) lần lượt lấy các điểm \(E,D\) sao cho \(AC = 3AE\) và \(AD = \frac{1}{3}AB\). Gọi \(I\) là giao điểm của \(BD\) và \(EC\). Biết rằng \(\Delta ABD \sim \Delta ACE\).
\(\widehat {ADB} = \widehat {AEC}\).
\(\frac{{AE}}{{AC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\).
\(\Delta ADE \sim \Delta ACB\).
\(ID.IB = IE.IC\).
Cho \(\Delta HAB\) vuông tại \(H\) có \(HA = 4\,\,{\rm{cm}},\,\,BH = 6\,\,{\rm{cm}}.\)Trên tia đối của tia \(HA\) lấy điểm \(C\) sao cho \(HC = 9\,\,{\rm{cm}}{\rm{.}}\)
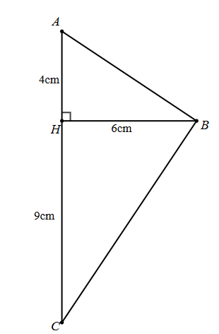
Khi đó:
a) \(\frac{{AH}}{{BH}} = \frac{{HB}}{{HC}} = \frac{2}{3}.\)
b) \(\Delta AHB \sim \Delta HBC\).
c) \(\widehat {ABH} = \widehat {BCH}\).
d) \(\Delta ABC\) vuông tại \(B.\)
\(\frac{{AH}}{{BH}} = \frac{{HB}}{{HC}} = \frac{2}{3}.\)
\(\Delta AHB \sim \Delta HBC\).
\(\widehat {ABH} = \widehat {BCH}\).
\(\Delta ABC\) vuông tại \(B.\)
Cho hình thoi \(ABCD\) có \(\widehat A = 60^\circ .\) Qua \(C\) kẻ đường thẳng \(d\) cắt tia đối của các tia \(BA,DA\) theo thứ tự ở \(E,\,F\).

Khi đó,
\(\frac{{EB}}{{BA}} = \frac{{EC}}{{CF}}\).
\(\frac{{EB}}{{BA}} = \frac{{DF}}{{AD}}\).
\(\widehat {EBD} = \widehat {BDF} = 120^\circ \).
\(\Delta EBD \sim \Delta BDF\).
Cho \(\Delta ABC\) có \(AB = 8\,\,\,{\rm{cm}},\,\,AC = 16\,\,{\rm{cm}}{\rm{.}}\) Gọi \(D\) và \(E\) là hai điểm lần lượt trên các cạnh \(AB,\,\,AC\) sao cho \(BD = 2\,\,{\rm{cm}},\,\,CE = 13\,\,{\rm{cm}}.\)
Khi đó,
\(\frac{{AB}}{{AC}} = \frac{{AE}}{{AD}}\).
\(\Delta AEB \sim \Delta ACD\).
\(\Delta AED \sim \Delta ABC\).
\(\widehat {AED} = \widehat {ACB}\).
Cho hình vuông \(ABCD.\) Trên cạnh \(BC\) lấy điểm \(E\). Tia \(AE\) cắt đường thẳng \(CD\) tại \(M,\) tia \(DE\) cắt \(AB\) tại \(N\). GỌI \(O\) là giao điểm của \(BM\) và \(CN\).

Khi đó:
\(\frac{{NB}}{{CB}} = \frac{{BC}}{{CM}}.\)
\(\Delta NBC \sim \Delta BMC\).
\(\widehat {BCN} = \widehat {COM}.\)
\(BM \bot CN.\)
Cho \(\Delta ABC\)và \(\Delta MNP\) có:
\(AB = 2\;\,{\rm{cm;}}\;\,AC = 4\;\,{\rm{cm;}}\;\,\widehat A = 50^\circ ;\;\,MN = 6\;\,{\rm{cm;}}\;\,MP = 12\;\,{\rm{cm;}}\;\,\widehat M = 50^\circ .\)
Tính tỉ số \(\frac{{BC}}{{NP}}.\) (Kết quả ghi dưới dạng số thập phân)
Cho \(\Delta ABC\) vuông tại \(A,\;\,\Delta MNP\) vuông tại \(M\) có \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = 5.\) Hỏi độ dài \(BC\) gấp bao nhiêu lần độ dài \(NP?\)
Cho tam giác \(ABC\) có \(AB = 6\;\,{\rm{cm,}}\;\,AC = 7,5\;\,{\rm{cm}}{\rm{.}}\) Trên các cạnh \(AB,\;\,AC\) lần lượt lấy các điểm \(M,\;\,N\) sao cho \(AM = 5\;\,{\rm{cm,}}\;\,AN = 4\;\,{\rm{cm}}{\rm{.}}\) Khi đó, \(\widehat {AMN} = ...\widehat C.\)
Tìm số thích hợp để điền vào “…” để được đáp án đúng.
Cho tam giác \(ABC\) có \(AB = 2\;\,{\rm{cm,}}\;\,AC = 4\;\,{\rm{cm}}{\rm{.}}\) Trên cạnh \(AC\) lấy điểm \(D\)sao cho \(AD = 1\;\,{\rm{cm}}{\rm{.}}\) Hỏi độ dài đoạn thẳng \(BC\) gấp bao nhiêu lần độ dài đoạn thẳng \(BD?\)
Cho hình vẽ:

Đơn vị đo độ dài là \({\rm{cm}}{\rm{.}}\) Hỏi \(\widehat {MAH}\) có số đo bằng bao nhiêu độ?
