20 câu trắc nghiệm Toán 8 Cánh diều Bài 33. Trường hợp đồng dạng thứ nhất của tam giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho \(\Delta ABC\) và \(\Delta MNP\) có \(\frac{{AB}}{{MN}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{PN}}\) thì
\(\Delta ABC \sim \Delta MNP.\)
\[\Delta ABC \sim \Delta MPN.\]
\(\Delta ABC \sim \Delta NMP.\)
\(\Delta ABC \sim \Delta PMN.\)
Cho \(\Delta ABC \sim \Delta MNP\). Biết \(AB = 2\,\,{\rm{cm}},\,\,BC = 3\,\,{\rm{cm}},\,\,MN = 6\,\,{\rm{cm, }}MP = 6\,\,{\rm{cm}}{\rm{.}}\) Khẳng định nào dưới đây là sai?
\(AC = 2\,\,{\rm{cm}}{\rm{.}}\)
\(NP = 9\,\,{\rm{cm}}{\rm{.}}\)
\(\Delta MNP\) cân tại \(M.\)
\(\Delta ABC\) cân tại \(C\).
Cho hình sau:
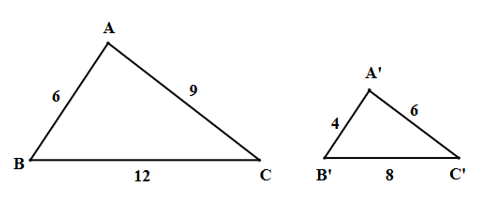
Khẳng định đúng là
\(\Delta ABC \sim \Delta A'B'C'\,\,\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right).\)
\(\Delta ABC \sim \Delta B'A'C'\,\,\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right).\)
\(\Delta BAC \sim \Delta A'B'C'\,\,\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right).\)
\(\Delta CAB \sim \Delta C'B'A'\,\,\,\,\left( {{\rm{c}}{\rm{.c}}{\rm{.c}}} \right).\)
Chọn khẳng định đúng.
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai tam giác đó có hai góc bằng nhau thì hai tam giác đó đồng dạng với nhau.
Cho \(\Delta ABC\) và \(\Delta MNP\) có \(AB = 2MN;\;\,MP = \frac{1}{2}AC;\;\,BC = 2NP\) thì
\(\Delta ABC \sim \Delta MNP.\)
\(\Delta ABC \sim \Delta MPN.\)
\(\Delta ABC \sim \Delta NMP.\)
\(\Delta ABC \sim \Delta PMN.\)
Cho hình vẽ:
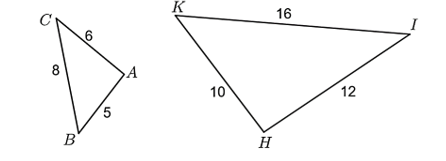
Khi đó:
\(\Delta ABC \sim \Delta HKI.\)
\(\Delta BCA \sim \Delta IKH.\)
\(\Delta CBA \sim \Delta KHI.\)
\(\Delta BAC \sim \Delta IHK.\)
Cho \(\Delta ABC \sim \Delta MNP\). Biết \(AB = 5\,\,{\rm{cm}},\,\,BC = 6\,\,{\rm{cm}},\,\,MN = 10\,\,{\rm{cm}}.\) Khẳng định nào dưới đây là đúng?
\(NP = 2,5\,\,{\rm{cm}},\,\,AC = 12\,\,{\rm{cm}}.\)
\(NP = 5\,\,{\rm{cm}},\,\,AC = 10\,\,{\rm{cm}}.\)
\(NP = 12\,\,{\rm{cm}},\,\,AC = 2,5\,\,{\rm{cm}}.\)
\(NP = 10\,\,{\rm{cm}},\,\,AC = 5\,\,{\rm{cm}}.\)
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là
\(4\,\,{\rm{cm, 5 cm, 6 cm}}\) và \(12\,\,{\rm{cm, 15 cm, 18 cm}}{\rm{.}}\)
\(3\,\,{\rm{cm, 4 cm, 6 cm}}\) và \(9\,\,{\rm{cm, 12 cm, 18 cm}}{\rm{.}}\)
\(1,5\,\,{\rm{cm, 2 cm, 2 cm}}\) và \(1\,\,{\rm{cm, 1 cm, 1 cm}}{\rm{.}}\)
\(14\,\,{\rm{cm, 15 cm, 16 cm}}\) và \(7\,\,{\rm{cm, 7,5 cm, 8 cm}}{\rm{.}}\)
Cho \(\Delta ABC \sim \Delta IKH\). Có bao nhiêu khẳng định đúng trong các khẳng định dưới đây?
(I). \(\frac{{HI}}{{AC}} = \frac{{KH}}{{BC}} = \frac{{KI}}{{AB}}.\) (II). \(\frac{{AB}}{{IK}} = \frac{{AC}}{{HI}} = \frac{{BC}}{{KH}}.\) (III). \(\frac{{AC}}{{HI}} = \frac{{AB}}{{KI}} = \frac{{HK}}{{BC}}.\)
0.
1.
2.
3.
Cho hai tam giác \(RSK\) và \(PQM\) có \(\frac{{RS}}{{PQ}} = \frac{{RK}}{{PM}} = \frac{{SK}}{{QM}}\). Khi đó, ta có:
\(\Delta RSK \sim \Delta PQM.\)
\(\Delta RSK \sim \Delta QPM.\)
\(\Delta RSK \sim \Delta MPQ.\)
\(\Delta RSK \sim \Delta QMP.\)
Cho \(\Delta ABC\) có \(AB = 4{\rm{ cm;}}\)\(BC = 8{\rm{ cm;}}\)\(AC = 6{\rm{ cm}}\). Một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) theo thứ tự \(M,N\) sao cho \(BM = AN\).
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
\(\Delta ABC \sim \Delta ANM\).
\(AN = 2,4{\rm{ cm}}\), \(MN = 3,2{\rm{ cm}}\).
\(\frac{{{S_{ANM}}}}{{{S_{ABC}}}} = \frac{4}{{25}}\).
Cho hình vẽ dưới đây:
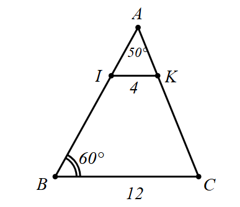
Biết rằng \(IK\parallel BC\) và \(AB = 15\,\,{\rm{cm}}\). Khi đó:
\(\Delta ABC \sim \Delta AIK\).
Tỉ số đồng dạng của \(\Delta ABC\) và \(\Delta AIK\) bằng \(\frac{1}{3}.\)
\(AI = 45\,\,{\rm{cm}}{\rm{.}}\)
\(\widehat {AKI} = 60^\circ .\)
Cho tứ giác \(ABCD\) có \(AB = 4\;\,{\rm{cm,}}\;\,AD = 6\;\,{\rm{cm,}}\;\,BD = 8\;\,{\rm{cm,}}\;\,BC = 12\;\,{\rm{cm,}}\;\,CD = 16\;\,{\rm{cm}}{\rm{.}}\)
\(\frac{{AB}}{{BD}} > \frac{{AD}}{{BC}} = \frac{{BD}}{{DC}}.\)
\(\Delta ABD \sim \Delta BDC\) với tỉ số đồng dạng là \(0,5.\)
\(\widehat {ABD} > \widehat {BDC}.\)
Tứ giác \(ABCD\) là hình thang có \(BC\) là đáy lớn.
Cho tứ giác \(ABCD\) có \(AB = 8\,\,{\rm{cm}},\,\,BC = 15\,\,{\rm{cm}},\,\,CD = 18\,\,{\rm{cm}},AD = 10\,\,{\rm{cm, }}BD = 12\,\,{\rm{cm}}{\rm{.}}\)
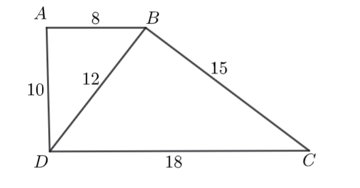
Khi đó:
\(\frac{{AB}}{{BD}} = \frac{{AD}}{{BC}} = \frac{{BD}}{{DC}}.\)
\(\Delta ABD \sim \Delta DBC.\)
\(AB\parallel CD.\)
\(ABCD\) là hình thang vuông.
Tứ giác \(ABCD\) có \(AB = 9\,\,{\rm{cm}},\,\,BC = 20\,\,{\rm{cm}},\,\,CD = 25\,\,{\rm{cm}},AD = 12\,\,{\rm{cm, }}BD = 15\,\,{\rm{cm}}{\rm{.}}\)
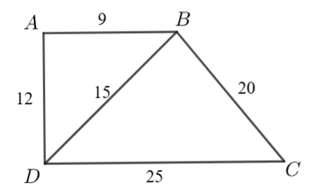
Khi đó:
\(\frac{{DB}}{{AB}} = \frac{{BC}}{{AD}} = \frac{{BD}}{{DC}}.\)
\(\Delta ABD \sim \Delta BDC\).
\(AB\parallel CD.\)
\(ABCD\) là hình thang cân.
Cho \(\Delta ABC \sim \Delta DEF\), biết \(AB = 3\,\,{\rm{cm}},\,\,AC = 5\,\,{\rm{cm, }}DE = 6\,\,{\rm{cm}}{\rm{.}}\) Hỏi độ dài cạnh \(DF\) bằng bao nhiêu? (Đơn vị: cm).
Cho \(\Delta MNP \sim \Delta DEF\) theo tỉ số đồng dạng bằng \(\frac{1}{2}\). Biết \(MN = 8\,\,{\rm{cm}},\,\,EF = 12\,\,{\rm{cm}}{\rm{.}}\) Hỏi độ dài \(NP\) bằng bao nhiêu? (Đơn vị: cm).
Cho tam giác nhọn \(ABC\,\,\left( {AB < AC} \right)\). Điểm \(M\) thuộc cạnh \(BC\) sao cho \(\frac{{MB}}{{MC}} = \frac{1}{2}\). Qua \(M\) kẻ đường thẳng song song với \(AB\) cắt \(AC\)ở \(E\). Biết rằng chu vi \(\Delta ABC\) bằng 24 cm.
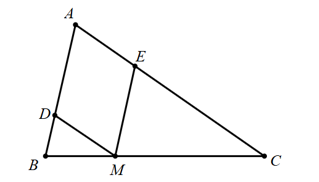
Tính tỉ số \(\frac{{BC}}{{MC}}\). (Kết quả ghi dưới dạng số thập phân)
Cho tam giác nhọn . Điểm thuộc cạnh sao cho . Qua kẻ đường thẳng song song với cắt ở . Biết rằng chu vi bằng 24 cm.

Tính chu vi \(\Delta EMC\). (Đơn vị: cm)
Cho tam giác nhọn . Điểm thuộc cạnh sao cho . Qua kẻ đường thẳng song song với cắt ở . Biết rằng chu vi bằng 24 cm.

Tính chu vi \(\Delta DBM\). (Đơn vị: cm)
