20 câu trắc nghiệm Toán 8 Cánh diều Bài 32. Tam giác đồng dạng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Nếu theo tỉ số đồng dạng 2 thì theo tỉ số đồng dạng
1
2
\(\frac{1}{2}.\)
\(\sqrt 2 .\)
Nếu thì
\(\widehat A = \widehat M.\)
\(\widehat A = \widehat N.\)
\(\widehat A < \widehat M.\)
\(\widehat A > \widehat M.\)
Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng bằng
1.
2.
\(\frac{1}{2}.\)
3.
Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}};\;\,\widehat {A'} = \widehat A;\;\,\widehat {B'} = \widehat B;\;\,\widehat {C'} = \widehat C\) thì
\(\Delta A'B'C' = \Delta ABC.\)
\(\Delta A'C'B' = \Delta ABC.\)
Nếu theo tỉ số đồng dạng 2 thì theo tỉ số đồng dạng
1
2
\(\frac{1}{2}.\)
\(\sqrt 2 .\)
Cho ; ; MP = 8cm. Độ dài cạnh \(NP\) bằng
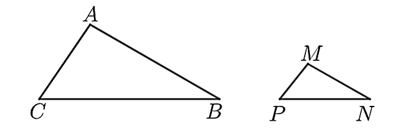
\(12\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
\(16\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC,\) một đường thẳng bất kì song song với \(BC\) cắt hai cạnh \(AB;\;\,AC\) lần lượt tại \(M\) và \(N.\) Khi đó:
Biết rằng và \(AB = 2A'B'.\) Khi đó:
\(\frac{{BC}}{{B'C'}} < 2.\)
\(\frac{{BC}}{{B'C'}} < \frac{1}{2}.\)
\(\frac{{BC}}{{B'C'}} = \frac{1}{2}.\)
\(\frac{{BC}}{{B'C'}} = 2.\)
Biết rằng khẳng định nào sau đây không đúng?
Biết rằng và \(\widehat B = 60^\circ ,\) khi đó:
\(\widehat I = 50^\circ .\)
\(\widehat I = 60^\circ .\)
\(\widehat I = 70^\circ .\)
\(\widehat I = 30^\circ .\)
Cho hình vẽ:
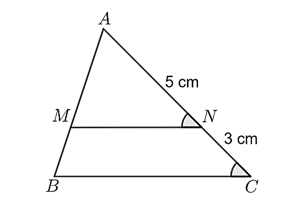
Biết rằng chu vi \(\Delta ABC\) bằng \(40\;\,{\rm{cm}}{\rm{.}}\) Khi đó:
\(MN\;{\rm{//}}\;BC.\)
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{5}{8}.\)
Chu vi \(\Delta MNP\) bằng \(30\;{\rm{cm}}{\rm{.}}\)
Cho hình vẽ sau.
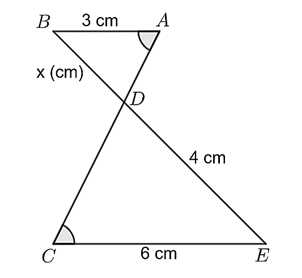
Khi đó:
\(AB\;{\rm{//}}\;CE.\)
\(\Delta DAB\) đồng dạng với \(\Delta DCE\) theo tỷ số đồng dạng bằng \(\frac{1}{2}.\)
\(x > 3\;\,{\rm{cm}}{\rm{.}}\)
Cho hình vẽ:
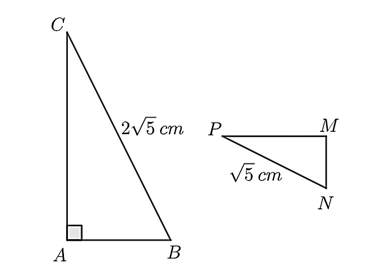
Biết rằng Khi đó:
\(\Delta MNP\) vuông tại \(M.\)
Diện tích \(\Delta MNP\) là \({S_{MNP}} = \frac{1}{4} \cdot PM \cdot MN.\)
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{PM}} = 4.\)
Diện tích \(\Delta ABC\) gấp 4 lần diện tích \(\Delta MNP.\)
Cho tam giác \(ABC\) có \(AB = 12\;\,{\rm{cm; }}AC = 18\;\,{\rm{cm}}{\rm{.}}\) Lấy các điểm \(M,\;N\) lần lượt trên các cạnh \(AB,\;\,AC\) sao cho \(AM = 8\;\,{\rm{cm; }}AN = 12\;\,{\rm{cm}}{\rm{.}}\) Lấy điểm \(P\) trên cạnh \(AC\) sao cho \(AP = 8\;\,{\rm{cm}}{\rm{.}}\)
\(MN\) không song song với \(BC.\)
\(\Delta APB = \Delta AMN.\)
Cho hình bình hành \(ABCD\) có \(E,\;\,F\) lần lượt là trung điểm của \(DC,\;\,AC.\)
\(EF\;{\rm{//}}\;AD.\)
\(\Delta CEF\) đồng dạng với \(\Delta CAD\) theo tỉ số đồng dạng \(\frac{2}{3}.\)
\(\Delta CAD = \Delta ACB.\)
\(\Delta CEF\) đồng dạng với \(\Delta ACB\) theo tỉ số đồng dạng \(\frac{1}{2}.\)
Cho tam giác \(ABC.\) Gọi \(M,\;\,N\) lần lượt là trung điểm của \(AB,\;\,AC.\) Tam giác \(ABC\) đồng dạng với tam giác \(AMN\) theo tỉ số đồng dạng là bao nhiêu?
Cho và \(\frac{{\widehat A}}{1} = \frac{{\widehat B}}{2} = \frac{{\widehat C}}{3}.\) Tính số đo góc \(M\) của \(\Delta MNP.\)
Cho. Biết rằng \(\widehat B + \widehat C = 90^\circ .\) Hỏi số đo góc \(M\) bằng bao nhiêu độ?
Biết rằng , . Hỏi diện tích \(\Delta ABC\) gấp bao nhiêu lần diện tích \(\Delta HIK?\)
Cho \(\Delta ABC\) đồng dạng với \(\Delta DEF\) và \(\widehat A = 40^\circ ;\;\,\widehat F = 70^\circ .\) Hỏi số đo \(\widehat E\) bằng bao nhiêu độ?
