10 CÂU HỎI
Hằng đẳng thức bình phương của một tổng là
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}.\)
\({\left( {A + B} \right)^2} = {A^2} - 2AB + {B^2}.\)
\({\left( {A + B} \right)^2} = {A^2} - 2AB - {B^2}.\)
\({\left( {A + B} \right)^2} = {A^2} + AB + {B^2}.\)
Chọn khẳng định đúng.
\(\left( {A + B} \right)\left( {A - B} \right) = {A^2} + 2AB + {B^2}.\)
\(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}.\)
\(\left( {A + B} \right)\left( {A - B} \right) = {A^2} - 2AB + {B^2}.\)
\(\left( {A + B} \right)\left( {A - B} \right) = {A^2} + {B^2}.\)
Viết biểu thức \(25{x^2} - 20xy + 4{y^2}\) dưới dạng bình phương của một hiệu ta được
\({\left( {5x - 2y} \right)^2}.\)
\({\left( {2x - 5y} \right)^2}.\)
\({\left( {25x - 4y} \right)^2}.\)
\({\left( {5x + 2y} \right)^2}.\)
Điền vào chỗ trống sau:
2.
8.
4.
16.
Hằng đẳng thức lập phương của một rổng là
\({\left( {A + B} \right)^3} = {A^2} + 2AB + {B^2}.\)
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}.\)
\({\left( {A + B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}.\)
\({\left( {A + B} \right)^3} = {A^3} + {A^2}B + A{B^2} + {B^3}.\)
Biết rằng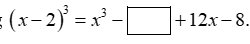 
Đơn thức thích hợp điền vào chỗ trống là
\(2{x^2}.\)
\(6{x^2}.\)
\( - 2{x^2}.\)
\( - 6{x^2}.\)
Hằng đẳng thức biểu diễn hiệu hai lập phương là
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}.\)
\({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} - AB - {B^2}} \right).\)
\({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right).\)
\({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} - AB + {B^2}} \right).\)
Viết \(\left( {3x - 2} \right)\left( {9{x^2} + 6x + 4} \right)\) dưới dạng hiệu ta được:
\(27{x^3} - 8.\)
\(27{x^3} + 8.\)
\(9{x^3} - 2.\)
\(3{x^3} - 2.\)
Biểu thức \(\frac{1}{4}{x^2}{y^2} + xy + 1\) bằng
\({\left( {\frac{1}{4}xy + 1} \right)^2}.\)
\({\left( {\frac{1}{2}xy + 1} \right)^2}.\)
\({\left( {xy - \frac{1}{2}} \right)^2}.\)
\({\left( {\frac{1}{2}xy - 1} \right)^2}.\)
Kết quả của tích \(\left( {{a^2} + 2a + 4} \right)\left( {a - 2} \right)\) là
\({\left( {a + 2} \right)^3}\).
\({\left( {a - 2} \right)^3}.\)
\({a^3} - 8.\)
\({a^3} + 8.\)