20 câu trắc nghiệm Toán 8 Cánh diều Bài 28. Định lí Thalès trong tam giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Hai đoạn thẳng \(AB\) và \(CD\) gọi là tỉ lệ với hai đoạn thẳng \({A_1}{B_1}\) và \({C_1}{D_1}\) nếu:
\(\frac{{AB}}{{{C_1}{D_1}}} = \frac{{{A_1}{B_1}}}{{CD}}.\)
\(\frac{{AB}}{{CD}} = \frac{{{A_1}{B_1}}}{{{C_1}{D_1}}}.\)
\(\frac{{CD}}{{{A_1}{B_1}}} = \frac{{AB}}{{{C_1}{D_1}}}.\)
\(\frac{{{A_1}{B_1}}}{{{C_1}{D_1}}} = \frac{{CD}}{{AB}}.\)
Biết rằng tỉ số của hai đoạn thẳng \(AB\) và \(CD\) là \(\frac{{AB}}{{CD}} = \frac{3}{5}\) và \(AB = 15\;{\rm{cm}}{\rm{.}}\) Tính độ dài đoạn thẳng \(CD.\)
\(CD = 25\;{\rm{cm}}{\rm{.}}\)
\(CD = 20\;{\rm{cm}}{\rm{.}}\)
\(CD = 10\;{\rm{cm}}{\rm{.}}\)
\(CD = 5\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC.\) Lấy điểm \(D\) thuộc cạnh \(AB,\) điểm \(E\) thuộc cạnh \(AC.\) Để \(DE\;{\rm{//}}\;BC\) thì:
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\)
\(\frac{{AD}}{{AC}} = \frac{{AE}}{{AB}}.\)
\(\frac{{AD}}{{AB}} = \frac{{AC}}{{AE}}.\)
Cả A, B, C đúng.
Biết rằng \(AB = 1\;{\rm{dm,}}\;IK = 2\;{\rm{cm}}{\rm{.}}\) Tính tỉ số \(\frac{{IK}}{{AB}}.\)
\(2.\)
\(\frac{1}{2}\)
\(5.\)
\(\frac{1}{5}.\)
Cho \(AB = 8\;{\rm{cm}}.\) Lấy điểm \(C\) thuộc tia đối của tia \(BA\) sao cho \(BC = 4\;{\rm{cm}}{\rm{.}}\) Tính tỉ số \(\frac{{AB}}{{AC}}.\)
\(\frac{{AB}}{{AC}} = 2.\)
\(\frac{{AB}}{{AC}} = \frac{3}{2}.\)
\(\frac{{AB}}{{AC}} = \frac{2}{3}.\)
\(\frac{{AB}}{{AC}} = \frac{1}{2}.\)
Cho hình vẽ:
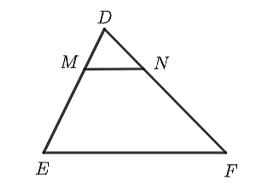
Biết rằng \(EF\;{\rm{//}}\;MN,\;MD = 20\;{\rm{cm,}}\;ND = 25\;{\rm{cm}},\;NF = 50\;{\rm{cm}}.\) Khi đó:
\(ME = 25\;{\rm{cm}}.\)
\(ME = 50\;{\rm{cm}}.\)
\(ME = 40\;{\rm{cm}}.\)
\(ME = 30\;{\rm{cm}}.\)
Cho các đoạn thẳng \(EF = 12\;{\rm{cm}},\;GH = 6\;{\rm{cm}},\;IK = 10\;{\rm{cm}},\;MN = x\;{\rm{cm}}.\) Để hai đoạn thẳng \(EF\) và \(GH\) tỉ lệ với hai đoạn thẳng \(IK\) và \(MN\) thì:
\(x = 15\;{\rm{cm}}{\rm{.}}\)
\(x = 5\;{\rm{cm}}{\rm{.}}\)
\(x = 2,5\;{\rm{cm}}{\rm{.}}\)
\(x = 20\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(\frac{{AD}}{{AB}} = \frac{3}{4}.\) Qua \(D\) kẻ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E.\) Khi đó:
\(\frac{{EC}}{{AE}} = \frac{1}{4}.\)
\(\frac{{EC}}{{AE}} = \frac{1}{2}.\)
\(\frac{{EC}}{{AE}} = \frac{2}{3}.\)
\(\frac{{EC}}{{AE}} = \frac{1}{3}.\)
Cho \(\Delta DEF\) có \(DE = 28\;{\rm{cm,}}\;DF = 35\;{\rm{cm}}{\rm{.}}\) Lấy điểm \(M\) thuộc cạnh \(DE\) sao cho \(DM = 16\;{\rm{cm}}{\rm{.}}\) Qua \(M\) vẽ đường thẳng song song với \(EF\) cắt \(DF\) tại \(N\) thì:
\(DN = 25\;{\rm{cm}}{\rm{.}}\)
\(DN = 10\;{\rm{cm}}{\rm{.}}\)
\(DN = 15\;{\rm{cm}}{\rm{.}}\)
\(DN = 20\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) có \(BC = 15\;{\rm{cm}}{\rm{.}}\) Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(BM = 12\;{\rm{cm}}{\rm{.}}\) Trên cạnh \(AC\) lấy điểm \(N\) sao cho \(\frac{{AN}}{{NC}} = 4.\) Khi đó:
\(\widehat B = \frac{3}{4}\widehat {NMC.}\)
\(\widehat B = \frac{3}{2}\widehat {NMC.}\)
\(\widehat B = \widehat {NMC.}\)
\(\widehat B = \frac{2}{3}\widehat {NMC.}\)
Cho \(\Delta ABC.\) Lấy điểm \(D\) bất kì trên cạnh \(BC.\) Qua \(D\) kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(F.\) Qua \(D\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E.\)
Tứ giác \(AEDF\) là hình bình hành
\(\frac{{AE}}{{AB}} = \frac{{CD}}{{BC}}.\)
\(\frac{{ED}}{{AC}} = \frac{{BD}}{{BC}}.\)
\(\frac{{DF}}{{AB}} + \frac{{ED}}{{AC}} = 2.\)
Cho hình vẽ:
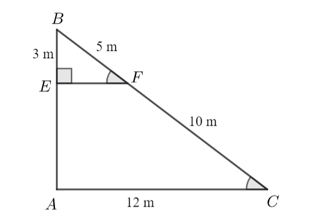
\(EF\;{\rm{//}}\;AC.\)
Tam giác \(ABC\) vuông tại \(A.\)
\(AB = 10\;{\rm{m}}{\rm{.}}\)
Diện tích tam giác \(ABC\)là \(54\;{{\rm{m}}^2}.\)
Cho hình vẽ:
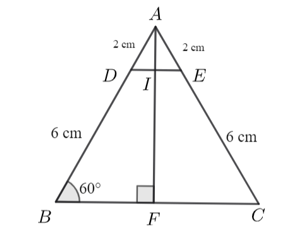
\(BC\;{\rm{//}}\;DE.\)
Tam giác \(ADE\) đều.
\(AI = \frac{1}{3}AF.\)
Diện tích tam giác \(ABC\) gấp bốn lần diện tích tam giác \(ADE.\)
Cho hình bình hành \(ABCD\) có \(M,\;N\)lần lượt là trung điểm của \(AB\) và \(CD.\) Gọi \(P,\;Q\) theo thứ tự là giao điểm của \(AN,\;CM\) với đường chéo \(BD.\)
Tứ giác \(AMCN\) là hình bình hành.
\(\frac{{BM}}{{MA}} = \frac{{BQ}}{{QP}}.\)
\(P\) là trung điểm của \(DQ.\)
\(DP = \frac{1}{4}BD.\)
Cho hình thang \(ABCD\;\left( {AB\;{\rm{//}}\;CD,\;AB < CD} \right).\) Gọi \(M\) là điểm thuộc cạnh \(AD\) sao cho \(\frac{{AM}}{{AD}} = \frac{1}{3}.\) Gọi \(I\) là điểm thuộc cạnh \(AC\) sao cho \(\frac{{AI}}{{IC}} = \frac{1}{2}.\) Gọi \(N\) là giao điểm của đường thẳng \(MI\) và cạnh \(BC.\)
\(\frac{{AM}}{{AD}} = \frac{{AI}}{{AC}}.\)
\(MN\;{\rm{//}}\;CD\;{\rm{//}}\;AB.\)
\(\frac{{CN}}{{CB}} = \frac{{CI}}{{CA}}.\)
\(\frac{{AM}}{{AD}} + \frac{{CN}}{{CB}} < 1.\)
Cho tam giác \(ABC\) có \(BC = 18\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC\) và \(G\) là trọng tâm của tam giác \(ABC.\) Qua \(G\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(M.\) Tính độ dài đoạn thẳng \(MD.\) (Đơn vị: \({\rm{cm}}\)).
Cho tam giác \(ABC\) có \(AC = 10\;{\rm{cm}}\) và điểm \(M\) là trung điểm của \(BC.\) Lấy điểm \(E\) thuộc \(AM\) sao cho \(EM = \frac{1}{3}EA.\) Tia \(BE\) cắt \(AC\) tại \(N.\) Tính độ dài đoạn thẳng \(AN.\) (Đơn vị: \({\rm{cm}}\)).
Cho tam giác \(ABC\) có \(AC = 22\,\;{\rm{cm}}\) và điểm \(D\) là thuộc cạnh \(BC\) sao cho \(\frac{{BD}}{{CD}} = 3,\) điểm \(E\) thuộc cạnh \(AD\) sao cho \(AE = \frac{1}{3}AD.\) Gọi \(K\) là giao điểm của \(BE\) và \(AC.\) Độ dài đoạn thẳng \(AK\) bằng bao nhiêu \({\rm{cm?}}\)
Cho tam giác \(ABC.\) Kẻ đường thẳng song song với \(BC\) cắt các cạnh \(AB,\;AC\) lần lượt tại \(H,\;K.\) Biết rằng \(\frac{{AH}}{{AB}} = \frac{1}{4}\) và \(AK + AC = 20\;{\rm{cm}}.\) Hỏi độ dài đoạn thẳng \(AK\) bằng bao nhiêu \({\rm{cm?}}\)
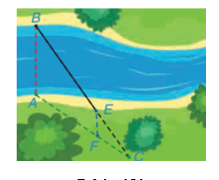
Để đo khoảng cách giữa hai vị trí \(E\) và \(B\)ở hai bên bờ sông, người ta tiến hành chọn các vị trí \(A,\;F,\;C\) cùng nằm trên một bên bờ sông sao cho ba điểm \(C,\;E,\;B\) thẳng hàng, ba điểm \(A,\;F,\;C\) thẳng hàng và \(EF\;{\rm{//}}\;AB.\) Người ta đo được \(AF = 80\;{\rm{m}},\;FC = 40\;{\rm{m}},\;CE = 60\;{\rm{m}}.\) Khoảng cách giữa hai vị trí \(E\) và \(B\) bằng bao nhiêu mét?