20 câu trắc nghiệm Toán 8 Cánh diều Bài 26. Phương trình bậc nhất một ẩn (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phương trình nào trong các phương trình dưới đây là phương trình một ẩn?
\({x^2} + {y^2} = 1.\)
\({x^2} = {z^2}.\)
\(xy = 1.\)
\({x^5} + {x^6} = 1.\)
Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) khi
\(A\left( {{x_0}} \right) \ge B\left( {{x_0}} \right).\)
\(A\left( {{x_0}} \right) \le B\left( {{x_0}} \right).\)
\(A\left( {{x_0}} \right) \ne B\left( {{x_0}} \right).\)
\(A\left( {{x_0}} \right) = B\left( {{x_0}} \right).\)
\(x = 1\) là nghiệm của phương trình
\(x + 1 = 0.\)
\({x^2} - 1 = 0.\)
\( - x - 1 = 0.\)
\({x^2} + 1 = 0.\)
Tập nghiệm của phương trình \(\frac{1}{2}\left( {x + 1} \right) = x + 2\) là
\(S = \left\{ 1 \right\}.\)
\(S = \left\{ 0 \right\}.\)
\(S = \left\{ 3 \right\}.\)
\(S = \left\{ { - 3} \right\}.\)
Nay nay mẹ 44 tuổi, gấp 4 lần tuổi của Lan năm ngoái. Gọi \(x\) là số tuổi của Lan năm nay thì phương trình ẩn \(x\) biểu thị cho điều này là
\(4x - 1 = 44.\)
\(4x = 44.\)
\(4\left( {x + 1} \right) = 44.\)
\(4\left( {x - 1} \right) = 44.\)
Phương trình nào dưới đây là phương trình bậc nhất một ẩn?
\(x + 5 = 0.\)
\(2{x^2} - 1 = 0.\)
\(0x + 5 = 0.\)
\(\frac{5}{x} = 0.\)
Tập nghiệm của phương trình \(2x = x - 5\) là
\(S = \left\{ { - 5;\;\, - 1} \right\}.\)
\(S = \left\{ { - 5;\;\,1} \right\}.\)
\(S = - 5.\)
\(S = \left\{ { - 5} \right\}.\)
Phương trình \(2\left( {{x^2} + 5} \right) + 2x = 2{x^2}\) có
0 nghiệm.
1 nghiệm.
2 nghiệm.
Vô số nghiệm.
Hình dưới đây mô tả một đài phun nước. Tốc độ ban đầu của nước là \(48\;\,{\rm{ft}}\,{\rm{/}}\,{\rm{s}}\) (\({\rm{ft}}\) là đơn vị đo độ dài với \(1\;\,{\rm{ft}} = 0,{\rm{3}}\;{\rm{048}}\;{\rm{m}}\)). Tốc độ \(v\;\left( {\,{\rm{ft}}\,{\rm{/}}\,{\rm{s}}} \right)\) của nước tại thời điểm \(t\;\,\left( {\rm{s}} \right)\) được cho bởi công thức \(v = 48 - 32t.\) Thời gian để nước đi từ mặt đài phun nước đến khi đạt vận tốc \(v = 16\;\,{\rm{ft}}\,{\rm{/}}\,{\rm{s}}\) là

1 giây.
2 giây.
3 giây.
\(1,5\) giây.
Cho phương trình: \(\frac{{x - 3}}{2} = \frac{{x - 1}}{3}.\) Khi đó, nghiệm của phương trình là số chia hết cho
3.
5.
7.
9.
Cho phương trình \({x^2} - 3x = {x^2} - x + 6\;\,\left( 1 \right).\)
Phương trình \(\left( 1 \right)\) là phương trình bậc nhất một ẩn.
\(x = 1\) là nghiệm của phương trình \(\left( 1 \right).\)
Phương trình \(\left( 1 \right)\) đưa được về phương trình \( - 2x = 6.\)
Phương trình \(\left( 1 \right)\) có hai nghiệm.
Cho hai phương trình ẩn \(x:\)\({x^2} - \left( {{x^2} - x} \right) + 5 = 0\;\,\left( 1 \right);\;\,4x = 4\left( {2x - k} \right)\;\,\left( 2 \right).\)
Biết rằng, phương trình \(\left( 1 \right)\) và phương trình \(\left( 2 \right)\) có cùng tập nghiệm.
\(x = - 2\) là một nghiệm của phương trình \(\left( 1 \right).\)
Phương trình \(\left( 1 \right)\) đưa được về dạng \(5 - x = 0.\)
Phương trình \(\left( 1 \right)\) có nghiệm là số nguyên âm.
\(k = 5.\)
Cho hình tam giác và hình chữ nhật có kích thước như hình vẽ (Đơn vị: \({\rm{cm}}\)):
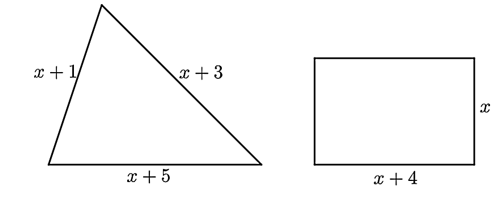
Biết rằng chu vi của hình tam giác và hình chữ nhật bằng nhau.
Chu vi tam giác là \(3x + 9\;\,\left( {{\rm{cm}}} \right).\)
Chu vi hình chữ nhật là \(2x + 8\;\,\left( {{\rm{cm}}} \right).\)
Phương trình biểu thị sự bằng nhau của chu vi hình tam giác và chu vi hình chữ nhật là \(3x + 9 = 2x + 8.\)
Có 1 giá trị của \(x\) để chu vi của hình tam giác và hình chữ nhật này bằng nhau.
Trong một cửa hàng bán thực phẩm, bác Lan nhìn thấy cô bán hàng dùng một chiếc cân đĩa. Bên đĩa thứ nhất, cô đặt hai quả cân, mỗi quả nặng \(500\;\,{\rm{g,}}\) bên đĩa thứ hai, cô đặt hai gói hàng cùng cân nặng \(x\;\,{\rm{g}}\) và bốn quả cân nhỏ, mỗi quả cân nặng \(50\;{\rm{g}}{\rm{.}}\) Bác Lan thấy cân thăng bằng.
Đĩa thứ nhất nặng \(500\;\,{\rm{g}}{\rm{.}}\)
Đĩa thứ hai nặng \(2x + 200\;\,\left( {\rm{g}} \right).\)
Phương trình biểu thị sự thăng bằng của cân là \(2x + 200 = 500.\)
Mỗi gói hàng nặng \(400\;\,{\rm{g}}{\rm{.}}\)
Cho hai phương trình: \(2{x^2} - 2 = 0\,\;\left( 1 \right);\;\,\frac{{{x^2} + 2}}{2} - \frac{1}{2}\left( {{x^2} + 2x + 2} \right) = 1\,\;\left( 2 \right).\)
\(x = 1\) là nghiệm của phương trình \(\left( 1 \right).\)
\(x = 1\) vừa là nghiệm của phương trình \(\left( 1 \right)\) vừa là nghiệm của phương trình \(\left( 2 \right).\)
Phương trình \(\left( 2 \right)\) có hai nghiệm.
Phương trình \(\left( 1 \right)\) và phương trình \(\left( 2 \right)\) có một nghiệm chung.
Tìm nghiệm của phương trình \(\frac{{x + 2}}{2} + \frac{{x + 1}}{4} = 5.\)
Cho \(A = 2x - 1;\;\,B = x + 3.\) Tìm giá trị của \(x\) để \(A - B = 5.\)
Phương trình \(2\left( {x - 1} \right) + 6 = 0\) có bao nhiêu nghiệm dương?
Cho phương trình: \(x + 3a = 10 + ax - a\,\;\left( 1 \right).\) Với giá trị nào của \(a\) thì \(x = 2\) là một nghiệm của phương trình \(\left( 1 \right)?\)
Tìm giá trị của \(x\) thỏa mãn phương trình: \(2\left( {x - 1} \right) - 6\left( {x + 5} \right) = - 3\left( {2x + 1} \right)\). (Kết quả ghi dưới dạng số thập phân)
