20 câu trắc nghiệm Toán 8 Cánh diều Bài 17. Hình bình hành (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)
Trong các hình dưới đây, hình nào là hình bình hành?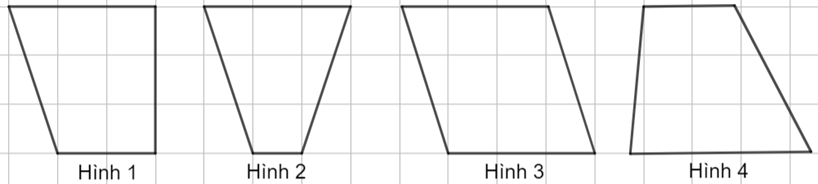
Hình \(1.\)
Hình \(2.\)
Hình \(3.\)
Hình \(4.\)
Trong hình bình hành:
Hai đường chéo vuông góc với nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hai đường chéo bằng nhau.
Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
Chọn câu sai:
Tứ giác có hai cặp cạnh đối song song là hình bình hành.
Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.
Tứ giác có hai đường chéo bằng nhau là hình bình hành.
Cho hình bình hành ABCD có \(\widehat {BAD} = 70^\circ .\) Khi đó:
\(\widehat {BCD} = 60^\circ .\)
\(\widehat {BCD} = 65^\circ .\)
\(\widehat {BCD} = 70^\circ .\)
\(\widehat {BCD} = 75^\circ .\).
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết rằng \(AC = 6\;{\rm{cm}}{\rm{.}}\) Tính độ dài đoạn thẳng \(OA.\)
\(OA = 3\;{\rm{cm}}.\)
\(OA = 4\;{\rm{cm}}.\)
\(OA = 2,5\;{\rm{cm}}.\)
\(OA = 1,5\;{\rm{cm}}.\)
Cho tứ giác \(ABCD\) có: \(\widehat A = \widehat C,\;\widehat B = \widehat D,\;AB = 3\;{\rm{cm}}{\rm{,}}\;AD = 5\;{\rm{cm}}{\rm{.}}\) Khi đó:
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{5}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
\(\frac{{DC}}{{BC}} = \frac{3}{4}.\)
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Biết rằng tổng độ dài của hai cạnh kề của một mắt lưới đó bằng \(9\;{\rm{cm}}{\rm{.}}\) Chu vi của một mắt lưới là: 
\(18\;{\rm{cm}}.\)
\(24\;{\rm{cm}}.\)
\(25\;{\rm{cm}}.\)
\(15\;{\rm{cm}}.\)
Chọn khẳng định đúng:
Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
Hình thang có hai cạnh bên bằng nhau là hình bình hành.
Hình thang có hai cạnh bên song song là hình bình hành.
Cả A, B, C đều đúng.
Cho tứ giác \(ABCD\) có hai đường chéo cắt nhau tại \[I.\] Nếu \(I\) vừa là trung điểm của \(AC\) và của \(BD\) thì:
\(\widehat {BAD} = \widehat {BCD}.\)
\(\widehat {BAD} = 2\widehat {BCD}.\)
\(2\widehat {BAD} = \widehat {BCD}.\)
\(\widehat {BAD} = 3\widehat {BCD}.\)
Cho tứ giác \(ABCD\) như hình vẽ:
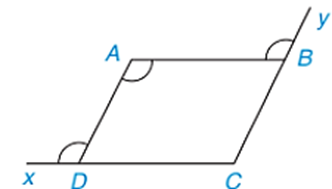
Biết rằng \(AD = 2\;{\rm{cm}}.\) Khi đó:
\(BC = 3\;{\rm{cm}}.\)
\(BC = 1,5\;{\rm{cm}}.\)
\(BC = 1\;{\rm{cm}}.\)
\(BC = 2\;{\rm{cm}}.\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Cho tứ giác \(ABCD\) như hình vẽ:
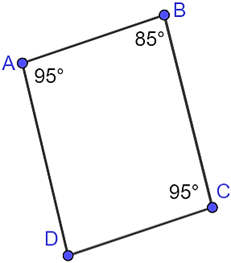
Biết rằng: \(AD - AB = 2\;{\rm{cm}},\;CD = \frac{3}{4}BC\)
a) \(\widehat D = 60^\circ .\)
b) Tứ giác \(ABCD\) là hình bình hành.
c) Gọi \(O\) là giao điểm của hai đường chéo trong tứ giác \(ABCD\) thì \(O\) là trung điểm của \(BD.\)
d) \(AD = 6\;{\rm{cm}}.\)
Cho hình bình hành \(ABCD.\) Gọi \(H,\;K\) lần lượt là hình chiếu vuông góc của \(A,\;C\) trên \(BD.\)
a) \(\widehat {ADB} = \widehat {DBC}.\)
b) \(\Delta DHA = \Delta BKC.\)
c) Tứ giác \(AKCH\) là hình bình hành.
d) \(\widehat {KAB} > \widehat {HCD}.\)
Cho tứ giác \(ABCD\) có \(AB\,{\rm{//}}\,CD,\;AB = CD,\;\widehat A - \widehat B = 50^\circ .\)
a) Tứ giác \(ABCD\) là hình bình hành.
b) \(\widehat A + \widehat B = 190^\circ .\)
c) \(\widehat C = 110^\circ .\)
d) \(\widehat D = 70^\circ .\)
Cho tam giác \(ABC\) có \(M,\;N\) lần lượt là trung điểm của \(AB,\;AC.\) Lấy điểm \(P\) sao cho \(N\) là trung điểm của đoạn thẳng \(MP.\)
a) \(\Delta ANM = \Delta CNP.\)
b) \(BM = CP.\)
c) Tứ giác \(BMPC\) là hình bình hành.
d) \(NP = \frac{1}{3}BC.\)
Cho hình bình hành\(ABCD\) có hai đường chéo cắt nhau tại \(O.\) Gọi \(M,\;N\) lần lượt là trung điểm của \(OB,\;OD.\)
a) \(OM = ON.\)
b) Tứ giác \(AMCN\) là hình bình hành.
c) \(AN > MC.\)
d) \(\widehat {DAN} = \widehat {MCB}.\)
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Cho tứ giác \(ABCD\) có \(\widehat {BAC} = \widehat {ACD}.\) Để tứ giác \(ABCD\) là hình bình hành thì \(AB = ...CD.\)
Tìm số thích hợp để điền vào “…”.
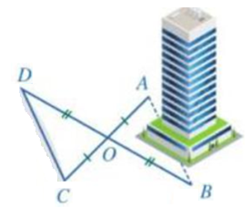
Để đo khoảng cách giữa hai vị trí \(A,\;B\) ở hai phía của một tòa nhà mà không thể đo được trực tiếp, người ta làm như sau: Chọn các vị trí \(O,\;C,\;D\) sao cho \(O\) không thuộc đường thẳng \(AB\) và khoảng cách \(CD\) là đo được và \(O\) là trung điểm của \(AC\) và \(BD.\) Người ta đo được \(CD = 150\;{\rm{m}}{\rm{.}}\) Độ dài \(AB\) bằng bao nhiêu \({\rm{m?}}\)
Cho hình bình hành\(ABCD\) có chu vi bằng \(30\;{\rm{cm}}{\rm{.}}\) Biết rằng chu vi tam giác \(ABD\) bằng \(27\;{\rm{cm}}{\rm{.}}\) Tính độ dài đường chéo \(BD.\) (Đơn vị: cm).
Cho tam giác \(ABC\) có \(AB = AC = 1,5\;{\rm{cm}}{\rm{.}}\) Từ điểm \(M\) thuộc cạnh \(BC,\) kẻ \(MD\) song song với \(AC\) và \(ME\) song song với \(AB\) (\(D,\;E\) lần lượt thuộc cạnh \(AB,\;AC\)). Chu vi tứ giác \(ADME\) bằng bao nhiêu \({\rm{cm}}?\)
Tính diện tích hình bình hành \(ABCD\) có đường chéo \(AC\) vuông góc với cạnh \(AD.\) Biết rằng \(AC = 12\;{\rm{cm}}{\rm{,}}\;AD = 9\;{\rm{cm}}{\rm{.}}\) (Đơn vị: \({\rm{c}}{{\rm{m}}^2}\)).
