20 câu trắc nghiệm Toán 8 Cánh diều Bài 16. Hình thang cân (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
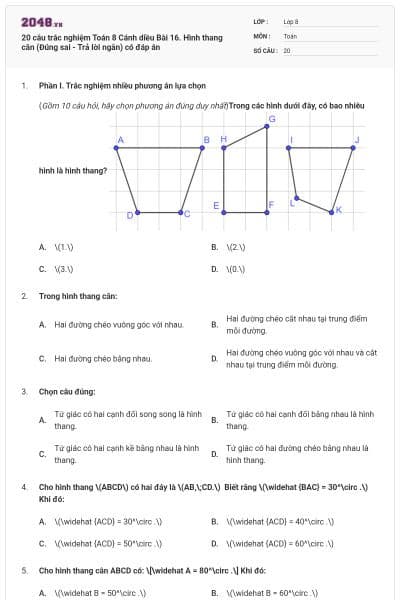
(Gồm 10 câu hỏi, hãy chọn phương án đúng duy nhất)Trong các hình dưới đây, có bao nhiêu hình là hình thang? 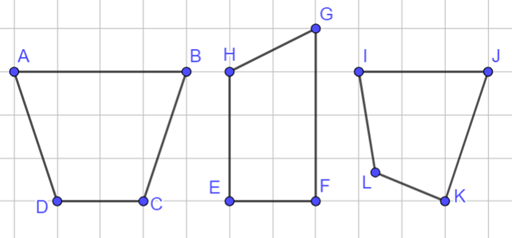
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Trong hình thang cân:
Hai đường chéo vuông góc với nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hai đường chéo bằng nhau.
Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
Chọn câu đúng:
Tứ giác có hai cạnh đối song song là hình thang.
Tứ giác có hai cạnh đối bằng nhau là hình thang.
Tứ giác có hai cạnh kề bằng nhau là hình thang.
Tứ giác có hai đường chéo bằng nhau là hình thang.
Cho hình thang \(ABCD\) có hai đáy là \(AB,\;CD.\) Biết rằng \(\widehat {BAC} = 30^\circ .\) Khi đó:
\(\widehat {ACD} = 30^\circ .\)
\(\widehat {ACD} = 40^\circ .\)
\(\widehat {ACD} = 50^\circ .\)
\(\widehat {ACD} = 60^\circ .\)
Cho hình thang cân ABCD có: \[\widehat A = 80^\circ .\] Khi đó:
\(\widehat B = 50^\circ .\)
\(\widehat B = 60^\circ .\)
\(\widehat B = 70^\circ .\)
\(\widehat B = 80^\circ .\)
Chọn câu sai trong các câu sau:
Hình thang có hai đường chéo bằng nhau là hình thang cân.
Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Hình thang có hai cạnh bên bằng nhau là hình thang cân.
Hình thang cân có hai cạnh bên bằng nhau.
Cho các tứ giác như hình vẽ dưới đây:
Các tứ giác nào là hình thang cân?
Tứ giác \(MNOP\) và tứ giác \(ABCD.\)
Tứ giác \(EHGF\) và tứ giác \(ABCD.\)
Tứ giác \(EHGF,\) tứ giác \(ABCD\) và tứ giác \(MNOP.\)
Cả bốn tứ giác đều là hình thang cân.
Một hình thang cân có chu vi bằng \(60\;{\rm{cm}}{\rm{,}}\) tổng hai đáy bằng \(40\;{\rm{cm}}\) thì độ dài cạnh bên là:
\(10\;{\rm{cm}}{\rm{.}}\)
\(20\;{\rm{cm}}{\rm{.}}\)
\(15\;{\rm{cm}}{\rm{.}}\)
\(5\;{\rm{cm}}{\rm{.}}\)
Cho tứ giác \(ABCD\) như hình vẽ dưới đây: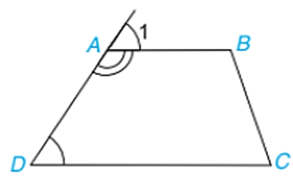
Tứ giác \(ABCD\) là hình thang có hai đáy là \(AB,\;CD.\)
Tứ giác \(ABCD\) là hình thang có hai đáy là \(AD,\;BC.\)
Tứ giác \(ABCD\) là hình thang có hai đáy là \(AC,\;BD.\)
Tứ giác \(ABCD\) không là hình thang.
Cho hình thang \(ABCD\) có một đáy là \(AB\) và \(AD \bot DC.\) Khi đó:
\[\widehat A = 70^\circ .\]
\[\widehat A = 80^\circ .\]
\[\widehat A = 75^\circ .\]
\[\widehat A = 90^\circ .\]
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Cho tứ giác \(ABCD\) có \(AB\,{\rm{//}}\,CD,\;AB < CD,\) \(AC = BD\) và \(\widehat {ABC} = 100^\circ .\)
a) Tứ giác \(ABCD\) là hình thang cân.
b) \(\widehat {DAB} = 110^\circ .\)
c) \(\widehat {ABC} + \widehat C = 180^\circ .\)
d) \(\widehat D = 80^\circ .\)
Cho \(\Delta ABC\) cân tại \(A.\) Các đường phân giác \(BD,\;CE\left( {D \in AC,\;E \in AB} \right).\) Biết rằng \(\widehat {ACB} = 55^\circ .\)
a) \(\Delta ADB = \Delta ACE.\)
b) \(DE\;{\rm{//}}\;BC.\)
c) Tứ giác \(BEDC\) là hình thang cân.
d) \(\widehat {BED} = 115^\circ .\)
Cho tứ giác \(ABCD\) có \(\widehat A = 125^\circ ,\;\widehat B - \widehat D = 90^\circ ,\;\widehat C = 35^\circ .\)
a) \(\widehat B + \widehat D = 310^\circ .\)
b) \(\widehat D = 85^\circ .\)
c) \(AB\,{\rm{//}}\,CD.\)
d) Tứ giác \(ABCD\) là hình thang cân.
Cho hình thang \(ABCD\;\left( {AB\,{\rm{//}}\,CD} \right)\) có \(\widehat {BAC} = \widehat {ABD}.\) Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
a) \(OA = OB.\)
b) Tam giác \(OCD\) cân tại \(C.\)
c) \(AC > BD.\)
d) \(AD = BC.\)
Cho tam giác \(ABC\) cân tại \(A.\) Kẻ các đường cao \(BE,\;CD\) của tam giác \(ABC.\)
a) Tam giác \(ADE\) cân tại \(A.\)
b) \(\widehat {ABC} > \widehat {ADE}.\)
c) \(DE\;{\rm{//}}\;BC.\)
d) Tứ giác \(BDEC\) là hình thang cân.
Phần III. Trắc nghiệm trả lời ngắn
(Gồm 5 câu hỏi, hãy viết câu trả lời/đáp án vào bài làm mà không cần trình bày lời giải chi tiết)
Cho hình thang cân \(ABCD\;\left( {AB\,{\rm{//}}\,CD} \right)\) có \(\widehat A = 2\widehat C.\) Số đo góc \(C\) bằng bao nhiêu độ?
Cho hình thang cân \(ABCD\;\left( {AB\,{\rm{//}}\,CD} \right).\) Biết rằng chu vi tam giác \(ABC\) bằng \(40\;{\rm{cm}}{\rm{.}}\) Hỏi chu vi tam giác \(ADB\) bằng bao nhiêu \({\rm{cm?}}\)
Cho hình thang cân \(ABCD\;\left( {AB\;{\rm{//}}\;CD} \right)\) có \(AB = 6\;{\rm{cm;}}\;CD = 12\;{\rm{cm}}.\) Kẻ \(AM \bot DC\) tại \(M\) và \(BN \bot DC\) tại \(N.\) Độ dài đoạn thẳng \(DN\) bằng bao nhiêu \({\rm{cm}}?\)
Cho hình thang cân \(ABCD\;\left( {AB\,{\rm{//}}\,CD,\;AB < CD} \right).\) Hai đường chéo cắt nhau tại \(P.\) Gọi \(Q\) là giao điểm của hai tia \(DA\) và \(CB.\) Gọi \(I\) là giao điểm của \(PQ\) và \(AB.\) Tính số đo góc \(QIB.\) (Đơn vị: Độ).
Cho hình thang \(ABCD\;\left( {AB\,{\rm{//}}\,CD} \right).\) Biết rằng \(\widehat B - \widehat C = 60^\circ ,\;\widehat C - \widehat D = 30^\circ .\) Số đo góc \(A\) bằng bao nhiêu độ?