20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 22. Hình có tâm đối xứng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Tâm đối xứng của hình thoi \(ABCD\) là
Giao điểm của hai đường chéo.
Trung điểm của \(AB.\)
Trung điểm của \(CD.\)
Điểm \(C.\)
Hình nào dưới đây là hình không có tâm đối xứng?
Hình vuông.
Hình chữ nhật.
Hình thoi.
Hình thang cân.
Cho hình vuông vẽ dưới đây:
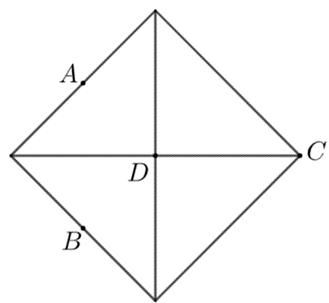
Điểm nào dưới đây là tâm đối xứng của hình trên?
Điểm \(A.\)
Điểm \(B.\)
Điểm \(C.\)
Điểm \(D.\)
Cho đoạn thẳng \(AB = 6\;{\rm{cm}}{\rm{.}}\) Gọi điểm \(O\) là tâm đối xứng của đoạn thẳng \(AB.\) Độ dài đoạn thẳng \(OA\) bằng
\(2\;{\rm{cm}}{\rm{.}}\)
\(3\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
\(1\;{\rm{cm}}{\rm{.}}\)
Cho các hình sau:
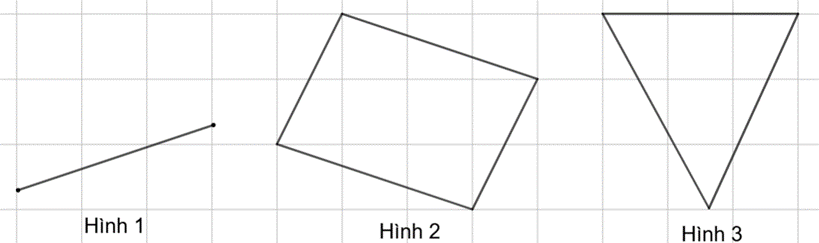
Hình nào là hình có tâm đối xứng?
Hình 1, Hình 3.
Hình 1, hình 2, hình 3.
Hình 1, Hình 2.
Hình 2, hình 3.
Chữ cái nào dưới đây có tâm đối xứng?

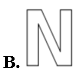
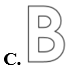

Cho hình vẽ:
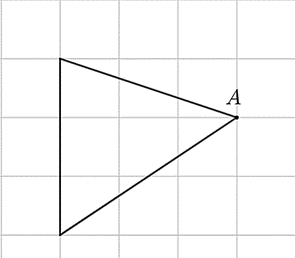
Cần vẽ thêm hình nào dưới đây để thu được một hình có điểm \(A\) là tâm đối xứng?
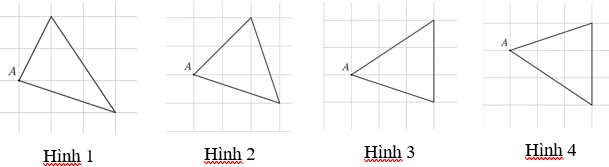
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Hình nào dưới đây có tâm đối xứng?
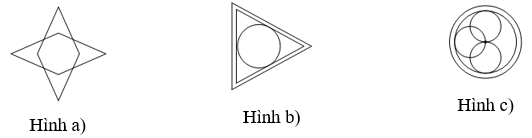
Hình a).
Hình b).
Hình a), Hình c).
Hình b), Hình c).
Hình nào dưới đây là hình có tâm đối xứng?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Chọn câu đúng.
Tâm đối xứng của hình lục giác đều \(ABCDEF\) là trung điểm của \(EB.\)
Tâm đối xứng của hình lục giác đều \(ABCDEF\) là trung điểm của \(AE.\)
Hình lục giác đều là hình không có tâm đối xứng.
Hình lục giác đều có hai tâm đối xứng.
Phần II. Trắc nghiệm đúng, sai
Cho các hình sau:
Hình vuông, hình chữ nhật, hình bình hành, hình thang cân, hình thoi, hình tròn.
Khi đó:
a)Tâm đối xứng của hình thang cân là giao điểm của hai đường chéo.
b)Tập hợp {Hình vuông; hình chữ nhật; hình bình hành} gồm các hình có tâm đối xứng.
c)Có 6 hình là hình có tâm đối xứng.
d)Có 4 hình vừa có tâm đối xứng vừa có trục đối xứng.
Cho đoạn thẳng \(AB = 8\;{\rm{cm}}{\rm{.}}\) Trục đối xứng của đoạn thẳng \(AB\) cắt đoạn thẳng đó tại điểm \(C.\) Trên đoạn thẳng \(CA\) lấy điểm \(E\) sao cho \(CE = 3\;{\rm{cm}}{\rm{.}}\) Trên đoạn thẳng \(CB\) lấy điểm \(D\) sao cho \(CD = 3\;{\rm{cm}}{\rm{.}}\)
a)\(C\) là trung điểm của đoạn thẳng \(AB.\)
b)\(C\) là tâm đối xứng đoạn thẳng \(AB.\)
c)\(C\) là không là trung điểm của đoạn thẳng \(ED.\)
d)\(C\) là tâm đối xứng của đoạn thẳng \(AB\) nhưng không là tâm đối xứng của đoạn thẳng \(ED.\)
Cho hình bình hành \(ABCD\) có tâm đối xứng là điểm \(O\) và \(OA = 6\;{\rm{cm}}{\rm{,}}\;\,OB = 4\;{\rm{cm}}{\rm{.}}\)
a)\(O\) là giao điểm của hai đường chéo \(AC\) và \(BD.\)
b)\(O\) vừa là trung điểm của \(AC\) vừa là trung điểm của \(BD.\)
c)\(AC = 12\;{\rm{cm}}{\rm{.}}\)
d)Tổng độ dài hai đường chéo của hình bình hành \(ABCD\) bằng \(30\;{\rm{cm}}{\rm{.}}\)
Cho hình chữ nhật \(ABCD\) và hình thoi \(EFGH\) như hình vẽ:
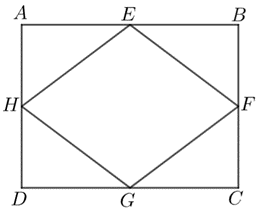
Khi đó:
a)Tâm đối xứng của hình chữ nhật \(ABCD\) là điểm \(F.\)
b)Hình thoi \(EFGH\) là hình có tâm đối xứng.
c)Hình thoi \(EFGH\) vừa có tâm đối xứng vừa có trục đối xứng.
d)Tâm đối xứng và trục đối xứng của hình thoi \(EFGH\) cũng là tâm đối xứng và trục đối xứng của hình chữ nhật \(ABCD.\)
Bàn cờ vua hình vuông gồm 8 hàng (đánh số từ 1 đến 8), 8 cột (đánh các chữ số từ a đến h).
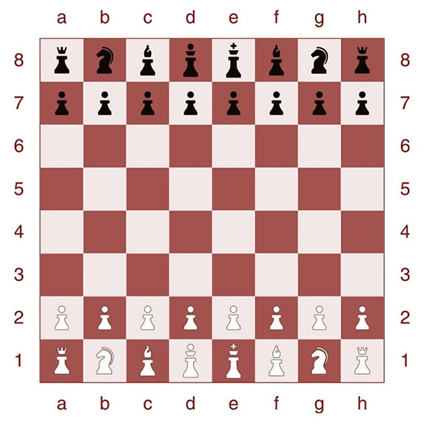
a)Bàn cờ vua có 5 trục đối xứng.
b)Tâm đối xứng của bàn cờ là giao điểm của 4 trục đối xứng.
c)Bàn cờ vua như trên là hình vừa có tâm đối xứng vừa có trục đối xứng.
d)Mã đen ở ô g8, có hình đối xứng qua tâm là mã trắng ở ô g1.
Phần III. Trắc nghiệm trả lời ngắn
Cho đoạn thẳng \(AB.\) Gọi điểm \(O\) là tâm đối xứng của đoạn thẳng \(AB.\) Khi đó, \(AO = ...OB.\)
Tìm số thích hợp để điền vào “…” để được câu đúng.
Có bao nhiêu hình không có tâm đối xứng trong các hình dưới đây?

Cho các hình như hình vẽ:

Có bao nhiêu hình có tâm đối xứng?
Cho các hình vẽ sau:

Có bao nhiêu hình vừa có tâm đối xứng vừa có trục đối xứng?
Cho các chữ cái sau:

Trong chữ cái trên, có bao nhiêu chữ cái vừa tâm đối xứng vừa có trục đối xứng?


