20 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 2. Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong các hình dưới đây, hình nào là hình bình hành?
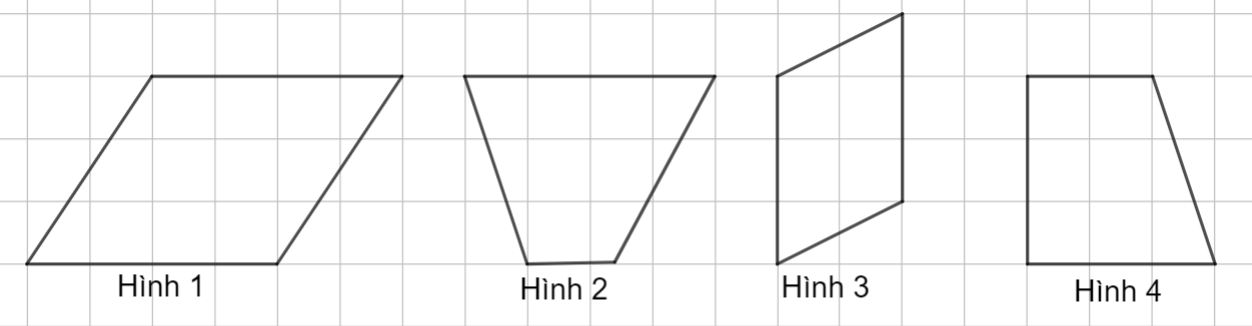
Hình 1.
Hình 1, Hình 3.
Hình 1, Hình 2.
Hình 1, Hình 2, Hình 4.
Người ta làm một cái đèn gỗ như hình vẽ:

Bốn mặt bên của đèn là bốn hình giống nhau. Bốn mặt bên đó gợi lên hình gì?
Hình vuông.
Hình thang cân.
Hình bình hành.
Hình thoi.
Hình nào sau đây có hai đường chéo bằng nhau?
Hình bình hành.
Hình thoi.
Hình thang.
Hình chữ nhật.
Hình nào dưới đây có bốn cạnh bằng nhau?
Hình bình hành.
Hình thoi.
Hình thang.
Hình chữ nhật.
Cho hình chữ nhật \(ABCD\) có \(CD = 6\;{\rm{cm}}{\rm{.}}\) Độ dài cạnh \(AB\) là
\(3\;{\rm{cm}}{\rm{.}}\)
\(4\;{\rm{cm}}{\rm{.}}\)
\(5\;{\rm{cm}}{\rm{.}}\)
\(6\;{\rm{cm}}{\rm{.}}\)
Mỗi góc trong hình chữ nhật bằng
\(70^\circ .\)
\(100^\circ .\)
\(90^\circ .\)
\(80^\circ .\)
Cho hình bình hành \(ABCD.\) Gọi \(O\) là giao điểm của hai đường chéo và \(OA = 3\;{\rm{cm}}{\rm{.}}\) Khi đó:
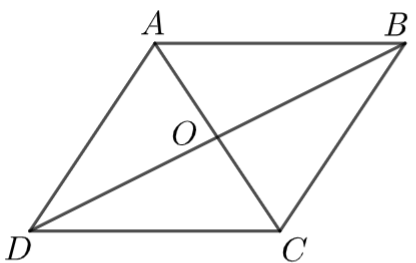
\(OC = 3\;{\rm{cm}}{\rm{.}}\)
\(OC = 4\;{\rm{cm}}{\rm{.}}\)
\(OC = 5\;{\rm{cm}}{\rm{.}}\)
\(OC = 6\;{\rm{cm}}{\rm{.}}\)
Cho hình thang cân \(ABCD\) có đáy lớn là \(AB.\) Chọn khẳng định đúng.
\(AB\) song song với \(CD.\)
\(AD\) song song với \(BC.\)
\(AC > BD.\)
\(AC < BD.\)
Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Số đo góc đỉnh \(O\) của tam giác \(AOB\) bằng
\(70^\circ .\)
\(100^\circ .\)
\(90^\circ .\)
\(80^\circ .\)
Cho hình bình hành \(ABCD\) có góc đỉnh \(B\) bằng \(56^\circ .\) Số đo góc đỉnh \(D\) của hình bình hành \(ABCD\) bằng
\(124^\circ .\)
\(28^\circ .\)
\(60^\circ .\)
\(56^\circ .\)
Vẽ đoạn thẳng \(AB = 4\;{\rm{cm}}{\rm{.}}\)
Vẽ đường tròn tâm \(A\) bán kính \(8\;{\rm{cm}}\) và đường tròn tâm \(B\) bán kính \(5\;{\rm{cm}}{\rm{.}}\) Hai đường tròn này cắt nhau tại \(C.\) Nối \(B\) với \(C.\)
Từ \(A\) kẻ đường thẳng song song với \(BC,\) từ \(C\) kẻ đường thẳng song song với \(AB.\) Hai đường thẳng này cắt nhau tại \(D.\)
(a)\(BC = 5\;{\rm{cm}}{\rm{.}}\)
(b)\(ABCD\) là hình bình hành.
(c)\(CD = 5\;{\rm{cm}}{\rm{.}}\)
(d) Tổng độ dài hai đoạn thẳng \(AD\) và \(CD\) bằng \(9\;{\rm{cm}}{\rm{.}}\)
Cho hai hình bình hành \(AECD\) và \(EBCD\) như hình vẽ:
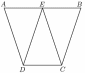
(a)\(AE\)và \(DC\) là hai cạnh kề nhau của hình bình hành \(AECD.\)
(b)\(AE = DC.\)
(c)\(EB > CD.\)
(d)\(E\)là trung điểm của \(AB.\)
Cho hình thoi \(ABCD\) như hình vẽ:
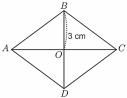
Biết rằng tam giác \(ABD\) là tam giác đều.
(a)\(O\) là trung điểm của \(BD.\)
(b)\(BD = 6\;{\rm{cm}}{\rm{.}}\)
(c)Độ dài cạnh tam giác \(ABD\) bằng \(6\;{\rm{cm}}{\rm{.}}\)
(d)\(DC > 8\;{\rm{cm}}{\rm{.}}\)
Cho hình vẽ sau:
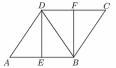
Biết rằng \(ABCD\) là hình bình hành, \(DEBF\) là hình chữ nhật.
(a)\(AB\) và \(DC\) là hai cạnh đối nhau của hình bình hành \(ABCD.\)
(b)\(AB > DC.\)
(c) Hình chữ nhật \(DEBF\) có các cạnh đối bằng nhau.
(d)\(FC = EA.\)
Cho hình thang cân \(ABCD\) có \(DC\) là đáy nhỏ, hai đường chéo cắt nhau tại \(O\) và \(OC = OD.\)
(a)\(BD\) và \(AB\) là hai đường chéo hình thang cân \(ABCD.\)
(b)\(BD\) đi qua điểm \(O.\)
(c)\(AC > BD.\)
(d)Tam giác \(AOB\) có hai cạnh bằng nhau.
Cho hình vẽ:
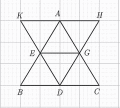
Hình vẽ trên có tất cả bao nhiêu hình bình hành?
Cho hình bình hành \(ABCD\) như hình vẽ có \(OA + OB = 12\;{\rm{cm}}{\rm{.}}\) Tính \(OC + OD.\) (Đơn vị: cm).
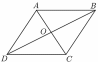
Một hình chữ nhật có tổng độ dài hai đường chéo bằng \(20\;{\rm{cm}}{\rm{.}}\) Độ dài mỗi đường chéo của hình chữ nhật đó bằng bao nhiêu \({\rm{cm?}}\)
Cho hình thoi \(ABCD\) có tổng số đo góc đỉnh \(A\) và đỉnh \(C\) bằng \(200^\circ .\) Số đo góc đỉnh \(A\) của hình thoi đó bằng bao nhiêu độ?
Cho hình vẽ:
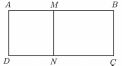
Biết rằng \(ADNM\) là hình vuông cạnh \(3\;{\rm{cm}}\) và \(ABCD\) là hình chữ nhật. Tính độ dài cạnh \(BC.\) (Đơn vị: \({\rm{cm}}\)).

