20 câu Trắc nghiệm Toán 6 Cánh diều Bài 11: Phân tích một số ra thừa số nguyên tố (Đúng sai - Trả lời ngắn) có đáp án
21 câu hỏi
Phân tích số 18 thành thừa số nguyên tố, ta được
\(18 = 10 + 8.\)
\(18 = 2 \cdot 9.\)
\(18 = 2 \cdot {3^2}.\)
\(18 = 3 \cdot 6.\)
Cho \(a = {2^2} \cdot 7\). Tập hợp tất cả các ước của \(a\) là
\(\left\{ {4;\,\,7} \right\}.\)
\(\left\{ {1;\,\,4;\,\,7} \right\}.\)
\(\left\{ {1;\,\,2;\,\,4;\,\,7;\,\,28} \right\}.\)
\(\left\{ {1;\,\,2;\,\,4;\,\,7;\,\,14;\,\,28} \right\}.\)
Một ước nguyên tố của 91 là
1.
2.
3.
7.
Cho \({a^2} \cdot b \cdot 7 = 140\) với \(a,b\) là các số nguyên tố.
Giá trị của \(a\) là
1.
2.
3.
4.
Giá trị của \(b\) là
1.
2.
5.
7.
Số 40 được phân tích thành tích các thừa số nguyên tố là
\(40 = 4 \cdot 10.\)
\(40 = 2 \cdot 20.\)
\(40 = {2^2} \cdot 5.\)
\(40 = {2^3} \cdot 5.\)
Số 225 chia hết cho tất cả bao nhiêu số nguyên tố?
2.
3.
5.
9.
Số các ước của số 192 là
7.
16.
14.
12.
Với giá trị nào dưới đây của \(p\) để \(p + 2;\,p + 4\) đều là các số nguyên tố?
2.
3.
5.
7.
Hai số 16 và 32 đều có chung ước nguyên tố nào?
2.
3.
5.
4.
Phân tích một số \(a\) ra thừa số nguyên tố theo chiều dọc ta được:
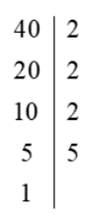
a) Số được phân tích là \(a = 40\).
b) Phân tích ta được \(a = 20 \cdot 10 \cdot 5 \cdot 1\).
c) Các ước nguyên tố của \(a\) là 2 và 5.
d) Tất cả các ước của \(a\) là \(\left\{ {1;\,\,2;\,\,4;\,\,5;\,\,8;\,\,10;\,\,20;\,\,40} \right\}\).
Phân tích số \(b\) ra tích các thừa số nguyên tố ta được:
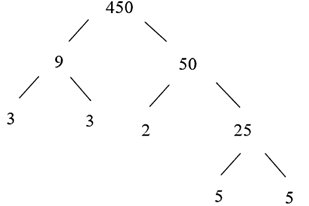
a) Số được phân tích là \(b = 450.\)
b) Phân tích ta được \(b = 2 \cdot {3^2} \cdot {5^2}.\)
c) Các ước nguyên tố của \(b\) là \(2;\,\,3;\,\,5;\,\,9\).
d) Số tròn chục duy nhất là ước của \(b\) là 50.
Cho hai số \(a\) và \(b.\) Biết rằng \(b\) là số nguyên tố và số \(a\) khi phân tích ra thừa số nguyên tố theo sơ đồ cột ta được:
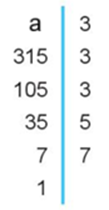
Tích của hai số \(a\) và \(b\)là một số chẵn. Khi đó:
a) \(a = {3^3} \cdot 5 \cdot 7.\)
b) \(a\) có bốn ước nguyên tố.
c) \(b = 2.\)
d) \(a + 4b\) là hợp số.
Cho số \(n = \overline {a2b.} \) Biết rằng \(b\) là số nguyên tố nhỏ nhất và \(a\) hợp số nhỏ nhất.
a) \(b = 3.\)
b) \(a = 4.\)
c) Số \(n\) là số nguyên tố.
d) Phân tích \(n - 2\) ra thừa số nguyên tố ta được \(n - 2 = {2^2} \cdot 3 \cdot 5 \cdot 7.\)
Cho \(a = 24 \cdot 15\) và \(b = 60.\)
a) Phân tích ra thừa số nguyên tố được \(b = 2 \cdot 3 \cdot 10\).
b) Số \(a\) khi phân tích ra thừa số nguyên tố được: \(a = {2^3} \cdot 9 \cdot 5.\)
c) \(a\) có 3 ước nguyên tố.
d) Số ước nguyên tố của \(a\) nhiều hơn số ước nguyên tố của \(b.\)
Số 84 có bao nhiêu ước nguyên tố?
Các số nguyên tố \(2;\,\,3;\,\,5;\,\,7\) cùng là ước của số nào trong các số sau: 84; 420; 90; 150; 315?
Hỏi số 424 có bao nhiêu ước có hai chữ số?
Một hình vuông có diện tích bằng \(1\,936\,\,{{\rm{m}}^2}\). Hỏi độ dài cạnh hình vuông đó bằng bao nhiêu mét?
Thực hiện phân tích số 360 thành tích các thừa số nguyên tố. Hỏi rằng tích đó xuất hiện bao nhiêu thừa số nguyên tố?



