20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài tập cuối chương V (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng \((P):x + 3y - 4z + 5 = 0?\)
\({\vec n_1} = (3;\;\;4;\;\;5).\)
\({\vec n_2} = (1;\;\;3;\;\; - 4).\)
\({\vec n_3} = (1;\;\;3;\;\;4).\)
\({\vec n_4} = (3;\;\; - 4;\;\;5).\)
Trong không gian Oxyz, mặt phẳng đi qua điểm \(K(1;\;\;1;\;\;1)\) nhận \(\vec u = (1;\;\;0;\;\;1),\)\(\vec v = (1;\;\;1;\;\;0)\) là cặp vectơ chỉ phương có phương trình tổng quát là:
\(x + y + z - 3 = 0.\)
\(x - y + z - 1 = 0.\)
\(x + y - z - 1 = 0.\)
\( - x + y + z - 1 = 0.\)
Trong không gian Oxyz, mặt phẳng cắt ba trục tọa độ tại ba điểm \(D(3;\;\;0;\;\;0),\;\)\[E(0;\;\; - 2;\;\;0),\;\]\(G(0;\;\;0;\;\; - 7)\)có phương trình chính tắc là:
\(\frac{x}{3} - \frac{y}{2} - \frac{z}{7} + 1 = 0.\)
\(\frac{x}{3} + \frac{y}{2} + \frac{z}{7} = 1.\)
\(\frac{x}{3} - \frac{y}{2} - \frac{z}{7} = 1.\)
\(\frac{x}{3} - \frac{y}{2} + \frac{z}{7} = 1.\)
Trong không gian \(Oxyz,\) đường thẳng đi qua điểm \(I(15;\;\; - 16;\;\;17)\) và nhận \(\vec u = ( - 7;\;\;8;\;\; - 9)\) là vectơ chỉ phương có phương trình tham số là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 15 - 7t}\\{y = - 16 + 8t}\\{z = 17 - 9t}\end{array}} \right..\)
\(\left\{ {\begin{array}{*{20}{l}}{x = 15 - 7t}\\{y = - 16 + 8t}\\{z = 17 - 9{t^2}}\end{array}} \right..\)
\(\left\{ {\begin{array}{*{20}{l}}{x = 15 - 7{t^2}}\\{y = - 16 + 8t}\\{z = 17 - 9t}\end{array}} \right..\)
\(\left\{ {\begin{array}{*{20}{l}}{x = - 7 + 15t}\\{y = 8 - 16t}\\{z = - 9 + 17t}\end{array}} \right..\)
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(\Delta :\frac{{x - 5}}{8} = \frac{{y - 9}}{6} = \frac{{z - 12}}{3}\)?
\({\vec u_1} = (8;\;\;6;\;\;3).\)
\({\vec u_2} = (8;\;\;6;\;\; - 3).\)
\({\vec u_3} = ( - 8;\;\;6;\;\; - 3).\)
\({\vec u_4} = (5;\;\;9;\;\;12).\)
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = - 4 + 2t}\\{y = 7 - 3t}\\{z = 8 - 9t}\end{array}} \right.\)?
\({\vec u_1} = (4;\;\;7;\;\;8).\)
\({\vec u_2} = ( - 4;\;\;7;\;\;8).\)
\({\vec u_3} = (2;\;\;3;\;\;9).\)
\({\vec u_4} = (2;\;\; - 3;\;\; - 9).\)
Trong không gian Oxyz, cho mặt cầu \((S):{\left( {x + 1} \right)^2} + {y^2} + {\left( {z - 3} \right)^2} = 4\). Tọa độ tâm I và bán kính R của mặt cầu (S) lần lượt là
\(I\left( { - 1;0;3} \right),R = 4\).
\(I\left( {1;0;3} \right),R = 4\).
\(I\left( { - 1;0;3} \right),R = 2\).
\(I\left( {1;0;3} \right),R = 2\).
Phương trình của mặt cầu \[\left( S \right)\] có tâm \[I\left( {2; - 1;3} \right)\], bán kính \[R = 4\] là
\[{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 3} \right)^2} = 16\].
\[{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 3} \right)^2} = 4\].
\[{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 4\].
\[{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 16\].
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai mặt phẳng \(\left( P \right):x - 2y + 2z - 1 = 0\) và \(\left( Q \right):2x + 2y - z - 3 = 0\). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Giá trị\[\cos \alpha \] bằng.
\[ - \frac{4}{9}\].
\[\frac{2}{3}\].
\[\frac{4}{9}\].
\[ - \frac{2}{3}\].
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng \(d:\frac{{x + 1}}{{ - 1}} = \frac{{y - 2}}{3} = \frac{{z - 1}}{3}\)?
\[Q\left( {1; - 2; - 1} \right)\].
\[A\left( {1;2;1} \right)\].
\[N\left( { - 1;3;2} \right)\].
\[P\left( { - 1;2;1} \right)\].
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Trong không gian Oxyz, cho hình lập phương \(ABCD.A\prime B\prime C\prime D\prime \) có \(A(0;\;0;\;0),\;\;B(2;\;0;\;0),\)\(D(0;\;2;\;0),\;\;A\prime (0;\;0;\;2).\) Gọi \(M,\;\;N\) lần lượt là trung điểm của \(AB\) và \(AA\prime \).
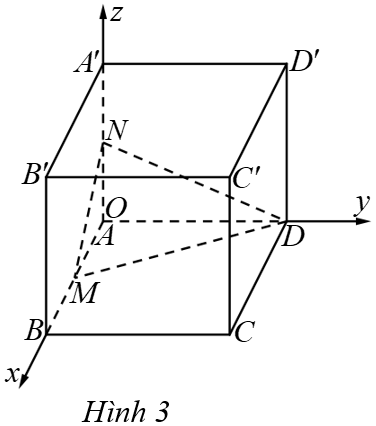
a) Toạ độ của điểm \(M\)là \((1;\;0;\;0).\)
b) Tọa độ của điểm \(N\)là \((0;\;1;\;0).\)
c) Phương trình mặt phẳng \((DMN)\) là: \(\frac{x}{1} + \frac{y}{2} + \frac{z}{1} = 1.\)
d) Khoảng cách từ điểm \(C\prime \) đến mặt phẳng \((DMN)\) bằng \(\frac{8}{3}.\)
Trong không gian Oxyz, cho hai mặt phẳng \((P):y = 0,\;\;(Q):\sqrt 3 x - y - 2024 = 0.\) Xét các vectơ \({\vec n_1} = (0;\;1;\;0),\;\;{\vec n_2} = (\sqrt 3 ;\; - 1;\;0).\)
a) \({\vec n_1}\) là một vectơ pháp tuyến của mặt phẳng \((P).\)
b) \({\vec n_2}\) không là vectơ pháp tuyến của mặt phẳng \((Q).\)
c) \({\vec n_1}.{\vec n_2} = - 1.\)
d) Mặt phẳng \((R)\)đi qua điểm \(M(1;1;1)\) và vuông góc \((P),(Q)\)có phương trình là\(\sqrt 3 x + y - z - \sqrt 3 = 0.\)
Trong không gian Oxyz, cho đường thẳng \(\Delta :\frac{{x - 2024}}{2} = \frac{y}{1} = \frac{{z + 2025}}{{ - 2}}\) và mặt phẳng \((P):2x + 2y - z + 1 = 0.\) Xét các vectơ \(\vec u = (2;\;1;\; - 2),\;\;\vec n = (2;\;2;\; - 1).\)
a) \(\vec u\) là một vectơ chỉ phương của đường thẳng \(\Delta .\)
b) \(\vec n\) là một vectơ pháp tuyến của mặt phẳng \((P).\)
c) Giao điểm của đường thẳng \(\Delta \) và mặt phẳng\((P)\) là \(M(2024;2025;1)\)
d) Mặt phẳng \((P): - 4x - 2y + 2z + 1 = 0\) vuông góc với đường thẳng \(\Delta \).
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x + 2y - z + 2 = 0\) và hai điểm \(A\left( {1;1;0} \right),\,\,B\left( {2;1;3} \right).\)
a) Một vec tơ pháp tuyến của \(\left( P \right)\) là \(\overrightarrow n = \left( {2;2;1} \right).\)
b) Đường thẳng \(d\) qua \(A\) và vuông góc với \(\left( P \right)\) có phương trình là \(\frac{{x - 1}}{2} = \frac{{y - 1}}{2} = \frac{z}{{ - 1}}.\)
c) Mặt cầu tâm \(A\) và tiếp xúc với mặt phẳng \(\left( P \right)\) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 4.\)
d) Gọi \(\alpha \)là góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( P \right).\) Khi đó, \(\sin \alpha = \frac{1}{{2\sqrt {10} }}.\)
Trong không gian Oxyz, cho mặt phẳng (P): \(2x + 2y - z + 3 = 0\) và các điểm \(A\left( {1;2;3} \right),B\left( {0; - 1;2} \right),C\left( {1;3; - 2} \right)\).
a) Điểm B cách mặt phẳng (P) một khoảng bằng 3.
b) Mặt phẳng (Q) đi qua điểm B và song song với mặt phẳng (P) có phương trình là \(2x + 2y - z - 4 = 0\).
c) Đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P) có phương trình tham số là \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + 2t\\z = 3 - t\end{array} \right.\).
d) Gọi H(a; b; c) là hình chiếu vuông góc của điểm C lên mặt phẳng (P). Khi đó giá trị của biểu thức \(T = a - b + 9c\) bằng −4.
PHẦN III. TRẢ LỜI NGẮN
Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng \((Oxy)\) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí \(A(5;\;0;\;5)\) đến vị trí \(B(10;\;10;\;3)\) và hạ cánh tại vị trí \(M(a;\;b;\;0).\) Giá trị của \(a + b\) bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?
Trong không gian Oxyz, cho tứ diện ABCD có \(A(5;\;3;\;6),\;\;B(1;\;1;\;4),\;\;C(2;\;1;\;2)\) và \(D(0;\;0;\;4).\) Khoảng cách từ điểm \(A\) đến mặt phẳng \((BCD)\) bằng bao nhiêu?
Trong không gian Oxyz, với mặt phẳng (Oxy) là mặt đất, một máy bay cất cánh từ vị trí A(0; 10; 0) với vận tốc \(\overrightarrow v = \left( {150;150;40} \right)\). Biết góc nâng của máy bay là \(\gamma = a^\circ \)(góc giữa hướng chuyển động bay lên của máy bay với đường băng và làm tròn kết quả đến hàng độ). Khi đó giá trị của a bằng bao nhiêu?
Trong không gian Oxyz (đơn vị trên mỗi trục là mét), một ngọn hải đăng được đặt ở vị trí I(21; 35; 50), biết rằng ngọn hải đăng được thiết kế với bán kính phủ sáng là 4 km. Giả sử người đi biển di chuyển theo một đường thẳng từ vị trí điểm I đến vị trí điểm D(5121; 658; 0). Khi người đi biển di chuyển đến điểm H(a; b; c) là điểm cuối cùng trên đoạn ID mà người đi biển có thể nhìn thấy ánh sáng từ ngọn hải đăng. Lúc đó c (cao độ của điểm H) có giá trị bằng bao nhiêu (kết quả làm tròn đến hàng đơn vị).
Trong không gian Oxyz, mặt cầu (S) có tâm I(1; 2; −3) và đi qua điểm A(3; −2; 1). Gọi M(1; 2; c) là điểm thuộc mặt cầu (S) biết \(c \in {\mathbb{N}^*}\). Cao độ điểm M có giá trị bằng bao nhiêu?
