10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình hộp ABCD.A'B'C'D'. Vectơ nào sau đây là vectơ đối của \(\overrightarrow {AB} \)?
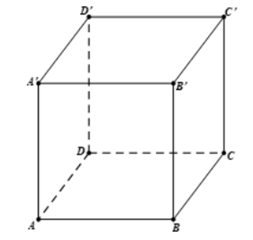
\(\overrightarrow {DC} \).
\(\overrightarrow {A'B'} \).
\(\overrightarrow {D'C'} \).
\(\overrightarrow {C'D'} \).
Cho hình hộp ABCD.A'B'C'D'. Số đo góc giữa hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CD} \) là
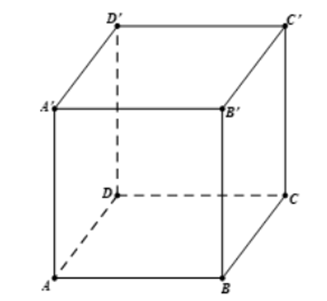
90°.
60°.
45°.
30°.
Cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh bằng 1. Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \)
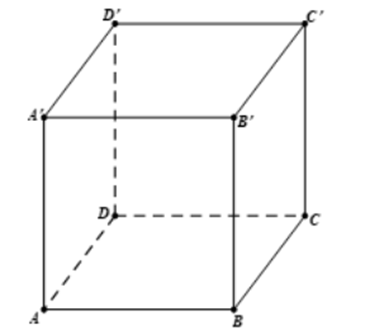
1.
−1.
0.
2.
Trong không gian Oxyz, cho hai điểm M(−5; 2; 3), I(2; 3; 1). Gọi N là điểm đối xứng với M qua I. Tính độ dài đoạn ON.
\(ON = 6\sqrt 2 \).
\(ON = 5\sqrt 2 \).
\(ON = 7\sqrt 2 \).
\(ON = 3\sqrt 2 \).
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = \left( {1;2;2} \right),\overrightarrow b = \left( {3;0; - 1} \right),\overrightarrow c = \left( { - 6;1; - 1} \right)\). Biết vectơ \(\overrightarrow m = 3\overrightarrow a - 2\overrightarrow b + \overrightarrow c \) có tọa độ (x; y; z). Tính T = x + y + z.
T = 6.
T = 5.
T = −5.
T = 7.
Cho tam giác ABC biết A(2; −1; 3) và trọng tâm của tam giác có tọa độ là G(2; 1; 0). Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} \) có tọa độ là
(0; −9; 9).
(0; 6; 9).
(0; 9; −9).
(0; 6; −9).
Trong không gian Oxyz, cho các điểm A(2; −1; 6), B(−3; −1; −4), C(5; −1; 0). Khẳng định nào sau đây đúng?
DABC cân.
DABC có 3 góc nhọn.
DABC vuông.
DABC đều.
Trong không gian Oxyz, cho hai vectơ là \(\overrightarrow a = \left( {1; - 2;3} \right)\) và \(\overrightarrow b = \left( { - 2;1;2} \right)\). Tích vô hướng \(\left( {\overrightarrow a + \overrightarrow b } \right).\overrightarrow b \) bằng
12.
2.
11.
10.
Trong không gian Oxyz, cho tam giác ABC với A(8; 9; 2), B(3; 5; 1), C(11; 10; 4). Số đo góc A của tam giác ABC là
120°.
30°.
150°.
60°.
Trong không gian Oxyz, cho A(2; 0; 0), B(0; 3; 1), C(−3; 6; 4). Gọi M là điểm nằm trên cạnh BC sao cho MC = 2MB. Độ dài đoạn AM bằng
\(3\sqrt 3 \).
\(2\sqrt 7 \).
\(\sqrt {30} \).
\(\sqrt {29} \).
