20 câu trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 9 thì có phương sai bằng
9.
3.
18.
81.
Một mẫu số liệu ghép nhóm có phương sai bằng 16 thì có độ lệch chuẩn bằng bao nhiêu?
4.
8.
256.
32
Khối lượng 66 quả bưởi da xanh ở lô hàng A được ghi lại ở bảng sau:
Khối lượng (kg) | [1,2; 1,4) | [1,4; 1,6) | [1,6; 1,8) | [1,8; 2,0) | [2,0; 2,2) | [2,2; 2,4) |
Số quả bưởi | 5 | 7 | 9 | 16 | 21 | 8 |
Khối lượng trung bình của mỗi quả bưởi gần nhất với kết quả nào dưới đây?
5.
8.
2.
3.
Số tiền ghi trên hóa đơn của 150 khách hàng lấy ngẫu nhiên trong một ngày của một siêu thị cho ở bảng dưới đây
Số tiền (nghìn đồng) | [50; 100) | [100; 150) | [150; 200) | [200; 250) | [250; 300) |
Tần số | 6 | 9 | 39 | 66 | 30 |
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên
49,24.
21,03.
24,25.
49,41.
Cho mẫu số liệu ghép nhóm về số tiền để mua 25 cây dừa giống như sau
Số tiền (nghìn đồng) | [0; 10) | [10; 20) | [20; 30) | [30; 40) | [40; 50) |
Số cây | 4 | 6 | 7 | 5 | 3 |
Phương sai của mẫu số liệu trên là
154,45.
154,56.
24,25
66,35.
Thống kê tổng số giờ nắng trong tháng 9 tại một trạm quan trắc đặt ở Thành phố Hồ Chí Minh trong các năm từ năm 2005 đến năm 2024 được thống kê như sau
Số giờ nắng | [80; 98) | [98; 116) | [116; 134) | [134; 152) | [152; 170) |
Số năm | 3 | 6 | 3 | 5 | 3 |
Phương sai của mẫu số liệu ghép nhóm trên gần nhất với con số nào sau đây?
566,6.
566.
566,
566,2.
Quãng đường đi bộ mỗi ngày (đơn vị: km) của thầy Minh trong 30 ngày được thống kê lại ở bảng sau.
Quãng đường (km) | [2,7; 3,0) | [3,0; 3,3) | [3,3; 3,6) | [3,6; 3,9) | [3,9; 4,2) |
Số ngày | 5 | 8 | 7 | 6 | 4 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm này gần nhất với con số nào sau đây?
0,38.
0,39.
0,4.
\(\frac{{2737}}{{18000}}\).
Cho bảng số liệu ghép nhóm về chiều cao đo được của 30 học sinh nam lớp 12A đầu năm học 2025 – 2026 của một trường THPT như sau
Chiều cao (cm) | [150; 155) | [155; 160) | [160; 165) | [165; 170) | [170; 175) |
Số học sinh | 3 | 7 | 10 | 7 | 3 |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm
5,63.
5,64.
5,65.
\(\sqrt {71} \).
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Độ dài quãng đường (km) | [50; 100) | [100; 150) | [150; 200) | [200; 250) | [250; 300) |
Số ngày | 5 | 10 | 9 | 4 | 2 |
Độ lệch chuẩn của mẫu số liệu ghép nhóm gần bằng
33,91.
155,15.
55,68.
36,54.
Khảo sát trọng lượng của một số quả mít được trồng trong một nông trường cho ta số liệu sau
Trọng lượng (kg) | [4; 6) | [6; 8) | [8; 10) | [10; 12) | [12; 14) |
Số quả | 6 | 12 | 19 | 9 | 4 |
Tìm độ lệch chuẩn của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm).
2,19.
8,72.
4,8.
2,2.
TRẮC NGHIỆM ĐÚNG – SAI
Thầy Tuấn thống kê lại điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:
Điểm trung bình | [5; 6) | [6; 7) | [7; 8) | [8; 9) | [9; 10) |
Lớp 11A | 1 | 0 | 11 | 22 | 6 |
Lớp 11B | 0 | 6 | 8 | 14 | 12 |
a) Nếu so sánh theo khoảng biến thiên thì điểm trung bình của các học sinh lớp 11B ít phân tán hơn điểm trung bình của các học sinh lớp 11A.
b) Khoảng biến thiên của điểm số học sinh lớp 11A là 5.
c) Xét mẫu số liệu của lớp 11A ta có độ lệch chuẩn của mẫu số liệu ghép nhóm là \(\sqrt {0,51} \).
d) Nếu so sánh theo độ lệch chuẩn thì học sinh lớp 11A có điểm trung bình ít phân tán hơn học sinh lớp 11B.
Bảng biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2021 tại Hà Nội (đơn vị: độ).
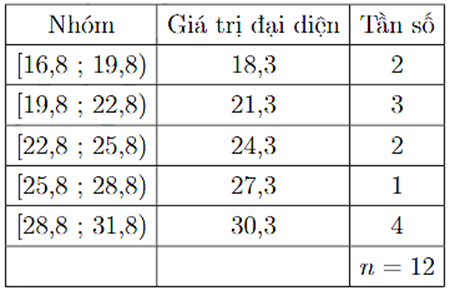
a) Khoảng biến thiên của mẫu số liệu trên là 15°C.
b) Số trung bình cộng của mẫu số liệu trên là 8,75°C.
c) Phương sai của mẫu số liệu trên là 25,8°C.
d) Độ lệch chuẩn của mẫu số liệu trên là 4,8°C.
Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực A và B.
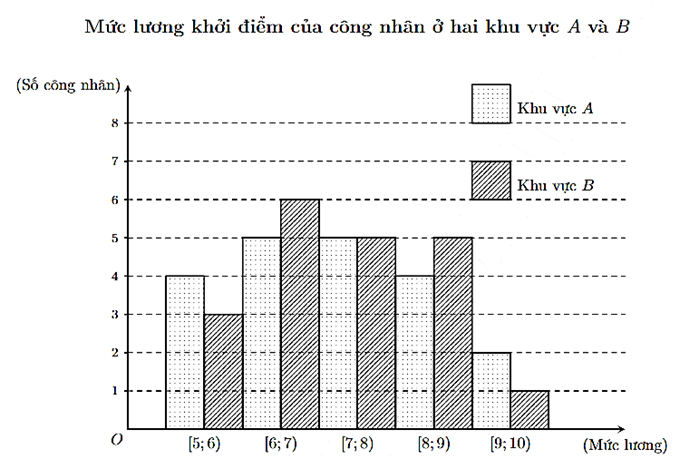
Người ta lập được bảng tần số ghép nhóm cho mẫu số liệu như sau
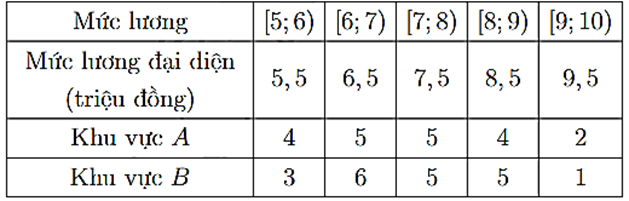
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là 4.
b) Xét mẫu số liệu của khu vực A ta có phương sai của mẫu số liệu ghép nhóm là 2,05.
c) Xét mẫu số liệu của khu vực B ta có phương sai của mẫu số liệu ghép nhóm là 1,5875.
d) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực B đồng đều hơn công nhân khu vực A.
Thống kê độ ẩm không khí trung bình các tháng năm 2021 tại Đà Lạt và Vũng Tàu (đơn vị: %) người ta thu được bảng số liệu ghép nhóm sau
Đà Lạt | Vũng Tàu | ||||||
Nhóm | Giá trị đại diện | Tần số | Nhóm | Giá trị đại diện | Tần số |
| |
\([75;78,3)\) | 76,65 | 0 | \([75;78,3)\) | 76,65 | 5 |
| |
\([78,3;81.6)\) | 79,95 | 2 | \([78,3;81.6)\) | 79,95 | 6 |
| |
\([81,6;84,9)\) | 83,25 | 1 | \([81,6;84,9)\) | 83,25 | 1 |
| |
\([84,9;88,2)\) | 86,55 | 6 | \([84,9;88,2)\) | 86,55 | 0 |
| |
\([88,2;91,5)\) | 89,85 | 3 | \([88,2;91,5)\) | 89,85 | 0 |
| |
a) Xét số liệu ở Đà Lạt ta có khoảng biến thiên là \(16,5\).
b) Xét số liệu ở Vũng Tàu thì khoảng tứ phân vị là \(0,23\) (làm tròn kết quả đến hàng phần trăm).
c) Xét số liệu ở Đà Lạt thì độ lệch chuẩn của mẫu số liệu ghép nhóm là \(3,28\)(làm tròn kết quả đến hàng phần trăm).
d) Đà Lạt có nhiệt độ không khí trung bình tháng đồng đều hơn so với ở Vũng Tàu vì có độ lệch chuẩn nhỏ hơn.
Bảng bên dưới cho ta bảng tần số ghép nhóm về số liệu thống kê tỉ lệ che phủ rừng (đơn vị: %) của 60 tỉnh, thành phố ở Việt Nam (không bao gồm Hưng Yên, Vĩnh Long, Cần Thơ tính đến ngày 31/12/2020.
Nhóm | \[\left[ {0;10} \right)\] | \[\left[ {10;20} \right)\] | \[\left[ {20;30} \right)\] | \[\left[ {30;40} \right)\] | \[\left[ {40;50} \right)\] | \[\left[ {50;60} \right)\] | \[\left[ {60;70} \right)\] | \[\left[ {70;80} \right)\] |
Tần số | 17 | 6 | 3 | 4 | 9 | 15 | 5 | 1 |
a) Mẫu số liệu trên có khoảng biến thiên \[R = 80.\]
b) Có 4 tỉnh, thành phố có tỉ lệ che phủ rừng nhỏ hơn \(40{\rm{\% }}\).
c) Khoảng tứ phân vị của mẫu số liệu đã cho bằng \[{\Delta _Q} = 53.\]
d) Tỉ lệ che phủ rừng trung bình trên các tỉnh, thành phố được thống kê là \[33,67\% \] và so với số này tỉ lệ che phủ rung trên các tỉnh, thành phố chênh lệch trung bình khoảng \[22,73\% .\]
PHẦN II. TRẢ LỜI NGẮN
Anh Minh đầu tư số tiền bằng nhau vào hai lĩnh vực A và B. Biểu đồ dưới đây mô tả số tiền thu được mỗi tháng trong vòng 60 tháng theo mỗi lĩnh vực A và B.
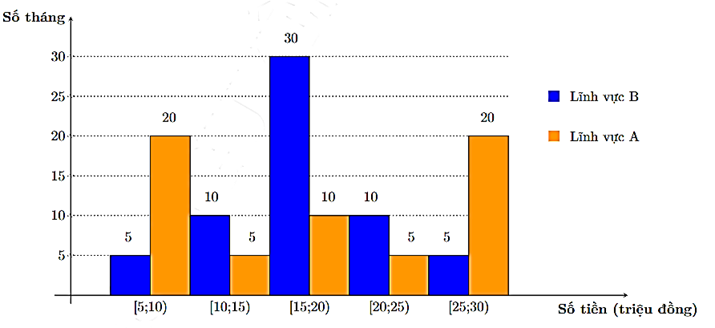
Hiệu độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào lĩnh vực A và B bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
Dưới đây là bảng thống kê thời gian tập thể dục của các em học sinh lớp 8A tại một trường THCS như sau:
Thời gian (phút) | [0; 10) | [10; 20) | [20; 30) | [30; 40) |
Số học sinh | 25 | 8 | 7 | 2 |
Phương sai của mẫu số liệu ghép nhóm trên (làm tròn kết quả hàng phần mười).
Chiều dài của 40 bé trai sơ sinh 12 ngày tuổi chọn ngẫu nhiên ở một bệnh viện được nhà nghiên cứu thông kê trong bảng dưới đây
Chiều dài (cm) | [44; 46) | [46; 48) | [48; 50) | [50; 52) | [52; 54) | [54; 56) |
Số trẻ | 3 | 3 | 10 | 15 | 7 | 2 |
Độ lệch chuẩn của chiều dài nhóm 40 bé trai sơ sinh (làm tròn kết quả đến hàng phần trăm).
Sau khi điều tra về cân nặng của 40 học sinh trong lớp 12A ở một trường THPT X thu được kết quả trong mẫu ghép nhóm sau:
Nhóm | Tần số |
\[\left[ {30;40} \right)\] | \[2\] |
\[\left[ {40;50} \right)\] | \[10\] |
\[\left[ {50;60} \right)\] | \[16\] |
\[\left[ {60;70} \right)\] | \[8\] |
\[\left[ {70;80} \right)\] | \[2\] |
\[\left[ {80;90} \right)\] | \[2\] |
| \[n = 40\] |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên ( làm tròn kết quả đến hàng phần chục).
Sau khi điều tra về số học sinh trong 100 lớp học, người ta chia mẫu số liệu đó thành 5 nhóm như sau:
Nhóm | Tần số |
\[\left[ {36;38} \right)\] | \[9\] |
\[\left[ {38;40} \right)\] | \[15\] |
\[\left[ {40;42} \right)\] | \[25\] |
\[\left[ {42;44} \right)\] | \[30\] |
\[\left[ {44;46} \right)\] | \[21\] |
| \[n = 100\] |
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên ( làm tròn kết quả đến hàng phần trăm).