20 câu trắc nghiệm Toán 12 Cánh diều Bài tập cuối chương II (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khẳng định nào sau đây sai?
\(\left| {\overrightarrow {BD} } \right| = a\sqrt 2 \).
\(\left| {\overrightarrow {BD'} } \right| = a\sqrt 3 \).
\(\overrightarrow {AC} + \overrightarrow {A'C'} = \overrightarrow 0 \).
\(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
Cho hình lập phương ABCD.A'B'C'D' có tâm O. Gọi I là tâm của hình vuông A'B'C'D' và M là điểm thuộc đoạn thẳng OI sao cho \(OM = \frac{1}{2}MI\) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
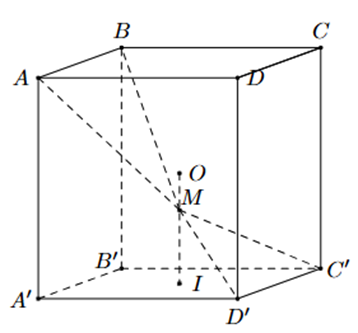
\(3\overrightarrow {IM} = \overrightarrow {OI} \).
\(\overrightarrow {MO} = \frac{1}{2}\overrightarrow {IM} \).
\(\overrightarrow {OM} = \overrightarrow {MI} \).
\(\overrightarrow {MI} = 2\overrightarrow {MO} \).
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng \(2\sqrt 3 \). Tính độ dài vectơ \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} \).
\(\sqrt 3 \).
\(\sqrt 2 \).
\(2\sqrt 6 \).
\(2\sqrt 2 \).
Trong không gian Oxyz, cho hai điểm B(3; 7; 5) và K(−1; −5; −7). Tọa độ vectơ \(\overrightarrow {BK} \) là
(−1; −12; −12).
(4; 12; 12).
(−4; −10; −12).
(−4; −12; −12).
Trong không gian Oxyz, cho hình vuông ABCD có B(3; 0; 8) và D(−5; −4; 0). Độ dài cạnh của hình vuông đã cho bằng
\(5\sqrt 2 \).
\(6\sqrt 2 \).
6.
12.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 1; 0), B(2; −1; 3). Tìm tọa độ điểm C trên trục Oy để tam giác ABC vuông tại
\(\left( {0;0;\frac{1}{2}} \right)\).
(0; 2; 0).
\(\left( {\frac{1}{2};0;0} \right)\).
\(\left( {0;\frac{1}{2};0} \right)\).
Trong không gian Oxyz, cho ba điểm A(3; 2; −1), B(1; −3; 2), C(−2; 1; 3). Khi đó tọa độ của vectơ \(\overrightarrow {AB} + 2\overrightarrow {AC} \) là
(−12; −7; 11).
(−9; −11; 10).
(12; 7; −11).
(−7; −6; 7).
Trong không gian với hệ tọa độ Oxyz, cho A(1; 1; 1) và B(2; −1; 2). Tọa độ điểm M thỏa mãn \(\overrightarrow {MA} - 2\overrightarrow {MB} = \overrightarrow 0 \) là
(3; −3; 3).
(−3; −3; 3).
(3; −3; −3).
(−3; 3; 3).
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD đáy ABCD là hình chữ nhật. Biết A(0; 0; 0), B(0; 4; 0), D(2; 0; 0), S(0; 0; 4). Gọi M là trung điểm của SB và G là trọng tâm của tam giác SCD. Độ dài MG là
\(MG = \frac{{\sqrt 6 }}{3}\).
\(MG = \frac{{\sqrt 6 }}{2}\).
\(MG = \frac{{2\sqrt 3 }}{3}\).
\(MG = \frac{{2\sqrt 6 }}{3}\).
Trong không gian với hệ trục Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;1;0} \right),\overrightarrow b = \left( { - 1;0; - 2} \right)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
\( - \frac{2}{{25}}\).
\( - \frac{2}{5}\).
\(\frac{2}{{25}}\).
\(\frac{2}{5}\).
Trong khônggian Oxyz, cho \(\overrightarrow a = \left( {2;1; - 2} \right)\) và \(\overrightarrow b = \left( {0;3;0} \right)\).
(a) Độ dài vectơ \(\overrightarrow a \) bằng 3.
(b) Tích vô hướng của hai vectơ \(\overrightarrow a ;\overrightarrow b \) là \(\overrightarrow a .\overrightarrow b = 5\).
(c) Tích có hướng của vectơ \(\overrightarrow a ;\overrightarrow b \) là \(\left[ {\overrightarrow a ,\overrightarrow b } \right] = \left( {6;0; - 4} \right)\).
(d) Vectơ \(\overrightarrow c = \left( {3;2; - 2} \right)\) vuông góc với \(\overrightarrow a = \left( {2;1; - 2} \right)\).
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a.
(a) Số vectơ bằng \(\overrightarrow {AB} \) có điểm đầu, điểm cuối là các đỉnh của hình lập phương đã cho là 5.
(b) \(\left| {\overrightarrow {D'A'} + \overrightarrow {B'B} } \right| = a\sqrt 3 \).
(c)\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AC'} \).
(d)\(\overrightarrow {AB} .\overrightarrow {DC'} = {a^2}\).
Trong không gian Oxyz, cho tam giác ABC với A(2; 1; 1), B(1; 2; 1) và C(−2; 2; 0).
(a) Số đo góc \(\widehat {BAC}\)làm tròn tới hàng phần mười theo đơn vị độ bằng 33,6°.
(b) Tọa độ trọng tâm G của tam giác ABC là \(G\left( {\frac{1}{3};\frac{5}{3};\frac{2}{3}} \right)\).
(c) Diện tích của tam giác ABC bằng \(\sqrt {11} \).
(d) Đường phân giác trong của góc \(\widehat {BAC}\) cắt cạnh BC tại điểm D có tọa độ là (a; b; c) thì a + b + c = 3.
Cho hình chóp \[ABCD\] có \[AB,AC,AD\] đôi một vuông góc, cạnh \[AB = AC = a\] ,\[M\] là trung điểm của \[CB\],\[H\] là trung điểm của \[MD\]. Các mệnh đề dưới đây đúng hay sai?
(a) \(\overrightarrow {DM} = \frac{{\overrightarrow {BD} + \overrightarrow {{\rm{CD}}} }}{{ - 2}}\).
(b) \(\overrightarrow {AH} = \frac{{\overrightarrow {AD} }}{2} + \frac{{\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} }}{4}\).
(c)\(\overrightarrow {AB} .\overrightarrow {AH} = \frac{{{a^2}}}{4}\).
(d) Góc giữa vectơ \[\overrightarrow {AH} \] và \(\overrightarrow {BC} \) bằng \(60^\circ \).
Trong không gian Oxyz, cho S(4; 2; 2) và các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) sao cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Khi đó:
(a)\(\overrightarrow {SA} = \left( {a - 4; - 2; - 2} \right),\overrightarrow {SB} = \left( { - 4;b - 2; - 2} \right),\overrightarrow {SC} = \left( { - 4; - 2;c - 2} \right)\).
(b) a = −3; b = 6; c = −6.
(c) SA = 3, SB = SC = 6.
(d) \({V_{S.ABC}} = 108\).
Cho hình hộp ABCD.A'B'C'D'. Biết A(1; −1; 1), B(1; 0; 1), C(2; 1; 2), D'(4; 5; −5). Một vectơ \(\overrightarrow v = \left( {a;b;1} \right)\) khác \(\overrightarrow 0 \) vuông góc với cả hai vectơ \(\overrightarrow {DD'} \) và \(\overrightarrow {D'A'} \). Tính −5a + 3b.
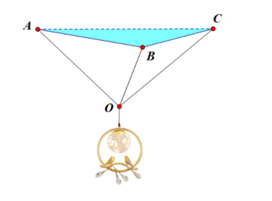
Người ta treo một chiếc đèn trang trí có trọng lượng 200 N lên trần nhà bằng ba sợi dây không dãn, bằng nhau tại ba điểm A, B, C tạo thành tam giác đều. Mỗi sợi dây tạo với mặt phẳng trần nhà một góc 30° đến được giữ ở trạng thái cân bằng (tham khảo hình vẽ). Hãy tính lực căng trong mỗi sợi dậy.
Trong không gian với hệ tọa độ cho trước (đơn vị đo lấy theo mét), một con ong bay từ điểm A(2; 4; 1) với vận tốc và hướng không đổi đến điểm B(10; 12; 5) trong 5 giây. Nếu con ong tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của con ông sau 3 giây tiếp theo đạt tại vị trí điểm M(a; b; c). Tìm 5a – b – c.
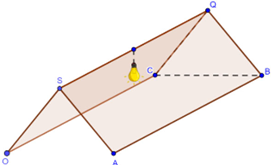
Hình bên dưới minh họa một cái lều hai mái là hai hình chữ nhật giống nhau trong không gian Oxyz. Biết các kích thước của mái lều là SA = 5m, AB = 10m, độ cao từ S xuống mặt đất là 4m. Bạn An muốn trang trí chiếc lều bằng cách treo các sợi dây cờ trang trí từ các góc lều O, A, B, C đến đuôi một chiếc đền treo từ vị trí chính giữa của SQ cách SQ 30 cm. Hỏi tổng chiều dài sợi dây cờ trang trí tối thiểu bạn An cần mua là bao nhiêu mét? (kết quả làm tròn đến hàng phần mười).
Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí A, máy bay cách vị trí điều khiển 300m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 100m (tham khảo hình vẽ). Một phút sau, máy bay ở vị trí B cách vị trí điều khiển 1200m về phía nam và 2100m về phía đồng, đồng thời cách mặt đấy 250 m.
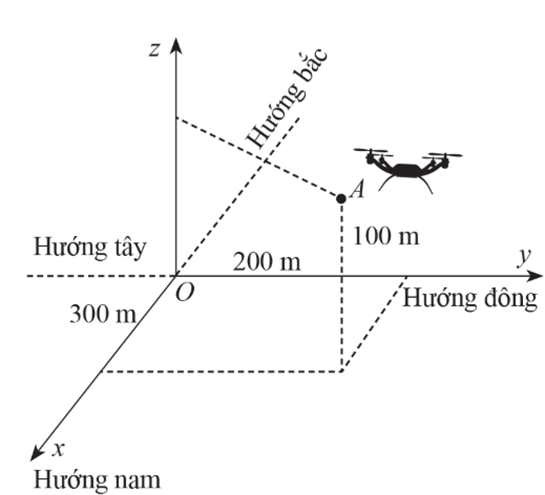
Chọn hệ trục tọa độ Oxyz với gốc O trùng với vị trí điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox có hướng trùng với hướng nam, trục Oy có hướng trùng với hướng đông, trục Oz vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên trục tương ứng với 1m. Khi đó tọa độ vectơ dịch chuyển \(\overrightarrow {AB} = \left( {a;b;c} \right)\) của máy bay không người lái đó. Tính a + b + c.