13 câu hỏi
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khẳng định nào sau đây sai?
\(\left| {\overrightarrow {BD} } \right| = a\sqrt 2 \).
\(\left| {\overrightarrow {BD'} } \right| = a\sqrt 3 \).
\(\overrightarrow {AC} + \overrightarrow {A'C'} = \overrightarrow 0 \).
\(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
Cho hình lập phương ABCD.A'B'C'D' có tâm O. Gọi I là tâm của hình vuông A'B'C'D' và M là điểm thuộc đoạn thẳng OI sao cho \(OM = \frac{1}{2}MI\) (tham khảo hình vẽ). Khẳng định nào sau đây đúng?
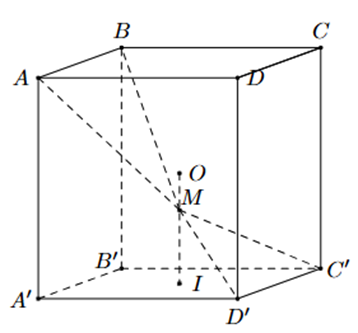
\(3\overrightarrow {IM} = \overrightarrow {OI} \).
\(\overrightarrow {MO} = \frac{1}{2}\overrightarrow {IM} \).
\(\overrightarrow {OM} = \overrightarrow {MI} \).
\(\overrightarrow {MI} = 2\overrightarrow {MO} \).
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng \(2\sqrt 3 \). Tính độ dài vectơ \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} \).
\(\sqrt 3 \).
\(\sqrt 2 \).
\(2\sqrt 6 \).
\(2\sqrt 2 \).
Trong không gian Oxyz, cho hai điểm B(3; 7; 5) và K(−1; −5; −7). Tọa độ vectơ \(\overrightarrow {BK} \) là
(−1; −12; −12).
(4; 12; 12).
(−4; −10; −12).
(−4; −12; −12).
Trong không gian Oxyz, cho hình vuông ABCD có B(3; 0; 8) và D(−5; −4; 0). Độ dài cạnh của hình vuông đã cho bằng
\(5\sqrt 2 \).
\(6\sqrt 2 \).
6.
12.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 1; 0), B(2; −1; 3). Tìm tọa độ điểm C trên trục Oy để tam giác ABC vuông tại
\(\left( {0;0;\frac{1}{2}} \right)\).
(0; 2; 0).
\(\left( {\frac{1}{2};0;0} \right)\).
\(\left( {0;\frac{1}{2};0} \right)\).
Trong không gian Oxyz, cho ba điểm A(3; 2; −1), B(1; −3; 2), C(−2; 1; 3). Khi đó tọa độ của vectơ \(\overrightarrow {AB} + 2\overrightarrow {AC} \) là
(−12; −7; 11).
(−9; −11; 10).
(12; 7; −11).
(−7; −6; 7).
Trong không gian với hệ tọa độ Oxyz, cho A(1; 1; 1) và B(2; −1; 2). Tọa độ điểm M thỏa mãn \(\overrightarrow {MA} - 2\overrightarrow {MB} = \overrightarrow 0 \) là
(3; −3; 3).
(−3; −3; 3).
(3; −3; −3).
(−3; 3; 3).
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.ABCD đáy ABCD là hình chữ nhật. Biết A(0; 0; 0), B(0; 4; 0), D(2; 0; 0), S(0; 0; 4). Gọi M là trung điểm của SB và G là trọng tâm của tam giác SCD. Độ dài MG là
\(MG = \frac{{\sqrt 6 }}{3}\).
\(MG = \frac{{\sqrt 6 }}{2}\).
\(MG = \frac{{2\sqrt 3 }}{3}\).
\(MG = \frac{{2\sqrt 6 }}{3}\).
Trong không gian với hệ trục Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;1;0} \right),\overrightarrow b = \left( { - 1;0; - 2} \right)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
\( - \frac{2}{{25}}\).
\( - \frac{2}{5}\).
\(\frac{2}{{25}}\).
\(\frac{2}{5}\).
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a.
(a) Số vectơ bằng \(\overrightarrow {AB} \) có điểm đầu, điểm cuối là các đỉnh của hình lập phương đã cho là 5.
(b) \(\left| {\overrightarrow {D'A'} + \overrightarrow {B'B} } \right| = a\sqrt 3 \).
(c)\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AC'} \).
(d)\(\overrightarrow {AB} .\overrightarrow {DC'} = {a^2}\).
(a) Số vectơ bằng \(\overrightarrow {AB} \) có điểm đầu, điểm cuối là các đỉnh của hình lập phương đã cho là 5.
(b) \(\left| {\overrightarrow {D'A'} + \overrightarrow {B'B} } \right| = a\sqrt 3 \).
(c)\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AC'} \).
(d)\(\overrightarrow {AB} .\overrightarrow {DC'} = {a^2}\).
Trong không gian Oxyz, cho S(4; 2; 2) và các điểm A(a; 0; 0), B(0; b; 0), C(0; 0; c) sao cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Khi đó:
(a)\(\overrightarrow {SA} = \left( {a - 4; - 2; - 2} \right),\overrightarrow {SB} = \left( { - 4;b - 2; - 2} \right),\overrightarrow {SC} = \left( { - 4; - 2;c - 2} \right)\).
(b) a = −3; b = 6; c = −6.
(c) SA = 3, SB = SC = 6.
(d) \({V_{S.ABC}} = 108\).
sao cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Khi đó:
(a)\(\overrightarrow {SA} = \left( {a - 4; - 2; - 2} \right),\overrightarrow {SB} = \left( { - 4;b - 2; - 2} \right),\overrightarrow {SC} = \left( { - 4; - 2;c - 2} \right)\).
(b) a = −3; b = 6; c = −6.
(c) SA = 3, SB = SC = 6.
(d) \({V_{S.ABC}} = 108\).
Trong không gian với hệ tọa độ cho trước (đơn vị đo lấy theo mét), một con ong bay từ điểm A(2; 4; 1) với vận tốc và hướng không đổi đến điểm B(10; 12; 5) trong 5 giây. Nếu con ong tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của con ông sau 3 giây tiếp theo đạt tại vị trí điểm M(a; b; c). Tìm 5a – b – c.
c.
