20 câu trắc nghiệm Toán 12 Cánh diều Bài 4. Ứng dụng hình học của tích phân (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Hình phẳng S gồm hai phần được đánh dấu trong hình vẽ bên. Diện tích hình S được tính theo công thức nào dưới đây
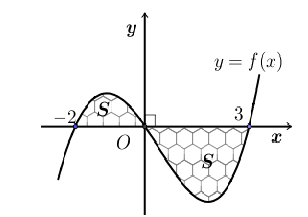
\(S = \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \).
\(S = - \int\limits_{ - 2}^0 {f\left( x \right)dx} - \int\limits_0^3 {f\left( x \right)dx} \).
\(S = - \int\limits_{ - 2}^0 {f\left( x \right)dx} + \int\limits_0^3 {f\left( x \right)dx} \).
\(S = \int\limits_{ - 2}^0 {f\left( x \right)dx} - \int\limits_0^3 {f\left( x \right)dx} \).
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2021\), trục hoành, \(x = - 2,x = 4\). Mệnh đề nào sau đây đúng.
\(S = \int\limits_{ - 2}^4 {\left| {{x^2} - 2021} \right|dx} \).
\(S = \int\limits_4^{ - 2} {\left| {{x^2} - 2021} \right|dx} \).
\(S = \int\limits_{ - 2}^4 {{{\left( {{x^2} - 2021} \right)}^2}dx} \).
\(S = \int\limits_{ - 2}^4 {\left( {{x^2} - 2021} \right)dx} \).
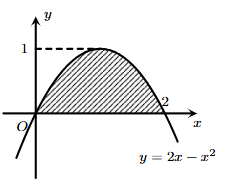
Cho hình phẳng D giới hạn bởi đồ thị \(\left( P \right):y = 2x - {x^2}\) và trục Ox. Tính thể tích của khối tròn xoay tạo thành khi cho D quay quanh trục Ox.
\(V = \frac{{17\pi }}{{15}}\).
\(V = \frac{{16\pi }}{{15}}\).
\(V = \frac{{19\pi }}{{15}}\).
\(V = \frac{{13\pi }}{{15}}\).
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 3\).
\(e\left( {{e^2} - 1} \right)\).
\({e^3} - 1\).
\({e^3}\).
\({e^2} - 1\).
Cho hình phẳng giới hạn bởi đồ thị hàm số \(f\left( x \right) = \cos \frac{x}{2}\), trục hoành và hai đường thẳng \(x = 0,x = \pi \). Thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox là
\({\pi ^2} - \pi \).
\(2\pi \).
\(\frac{{{\pi ^2}}}{2}\).
\({\pi ^2} - 1\).
Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau
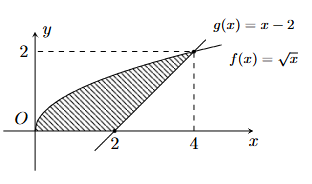
\(S = \frac{{16}}{3}\).
\(S = \frac{{10}}{3}\).
\(S = \frac{{11}}{3}\).
\(S = \frac{7}{3}\).
Diện tích hình phẳng giới hạn bởi trục Ox, trục Oy, đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(x = 2\) được tính theo công thức nào dưới đây?
\(\int\limits_2^0 {\left| {f\left( x \right)} \right|dx} \).
\(\int\limits_0^2 {\left| {f\left( x \right) - 2} \right|dx} \).
\(\int\limits_0^2 {f\left( x \right)dx} \).
\(\int\limits_0^2 {\left| {f\left( x \right)} \right|dx} \).
Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y = {x^2} + 3,y = 0,x = 0,x = 2\). Gọi \(V\) là thể tích khối tròn xoay được tạo thành khi quay \(\left( H \right)\)xung quanh trục \(Ox\). Mệnh đề nào sau đây đúng?
\(V = \pi \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \).
\(V = \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \).
\(V = \int\limits_0^2 {{{\left( {{x^2} + 3} \right)}^2}dx} \).
\(V = \pi \int\limits_0^2 {\left( {{x^2} + 3} \right)dx} \).
Cho hình phẳng \(D\)giới hạn bởi đường cong \(y = \sqrt {2 + \cos x} \), trục hoành và các đường thẳng \(x = 0;x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi \(D\)quay quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
\(V = \left( {\pi + 1} \right)\pi \).
\(V = \pi - 1\).
\(V = \pi + 1\).
\(V = \left( {\pi - 1} \right)\pi \).
Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = g\left( x \right),x = a,x = b\). Biết rằng \(f\left( x \right) - g\left( x \right) = - 8\). Mệnh đề nào dưới đây đúng?
\(S = \int\limits_a^b { - 8dx} \).
\(S = \int\limits_a^b {8dx} \).
\(S = \int\limits_a^b {64dx} \).
\(S = \pi \int\limits_a^b {64dx} \).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ {a;d} \right]\) và có đồ thị như hình vẽ. Biết đồ thị \(f\left( x \right)\) cắt trục hoành tại 4 điểm a, b, c, d đồng thời tạo với trục hoành và 2 đường thẳng \(x = a,x = d\) thành một hình phẳng (H) gồm 3 phần có diện tích lần lượt là S1; S2; S3 như hình vẽ.
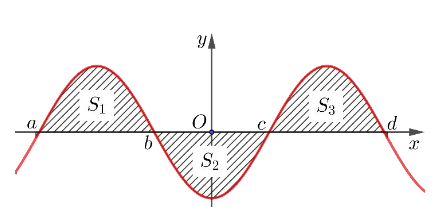
a) Hình phẳng có diện tích S3 khi quay quanh trục hoành tạo ra vật thể tròn xoay có thể tích là \(V = \int\limits_c^d {{{\left[ {f\left( x \right)} \right]}^2}dx} \).
b) Hình phẳng (H) khi quay quanh trục hoành tạo ra vật thể tròn xoay có thể tích là \(V = \pi \int\limits_a^d {{{\left[ {f\left( x \right)} \right]}^2}dx} \).
c) \({S_1} = \int\limits_a^b {f\left( x \right)dx} \).
d) \({S_2} = - \int\limits_b^c {f\left( x \right)dx} \).
Cho \({S_1},{S_2}\) là diện tích các hình phẳng được mô tả trong hình.
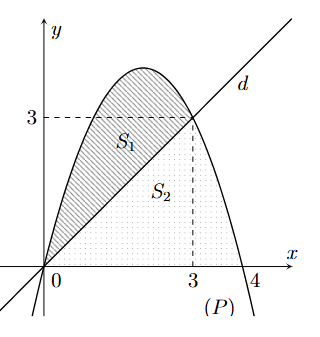
a) Phương trình đường thẳng d là \(y = x\).
b) Phương trình \(\left( P \right):y = - {x^2} - 4x\).
c) \({S_1} = \int\limits_0^3 {\left( { - {x^2} + 3x} \right)dx} \).
d) \(\frac{{{S_1}}}{{{S_2}}} = \frac{{27}}{{38}}\).
Cho hàm số \(f\left( x \right) = {x^2} - 2x\) có đồ thị là (C) và đường thẳng d: y = x.
a) Tích phân \(\int\limits_0^1 {f\left( x \right)dx} = - \frac{2}{3}\).
b) Hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x = 1, x = 2 có diện tích bằng \(\frac{4}{3}\).
c) Hình phẳng giới hạn bởi (C) và d có diện tích bằng \(\frac{9}{2}\).
d) Gọi (H) là hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng \(x = 0,x = 1\). Khối tròn xoay thu được khi cho (H) quay quanh trục hoành có thể tích bằng \(\frac{{8\pi }}{{15}}\).
Cho vật thể (T) giới hạn bởi hai mặt phẳng \(x = - 1;x = 1\). Cắt vật thể (T) bởi mặt phẳng vuông góc với trục \(Ox\) tại \(x\left( { - 1 \le x \le 1} \right)\) thu được thiết diện là một hình vuông có cạnh bằng \(2\sqrt {1 - {x^2}} \).
a) Mặt cắt có diện tích \(S\left( x \right)\) liên tục trên \(\left[ { - 1;1} \right]\).
b) Thể tích vật thể được tính theo công thức \(V = \pi \int\limits_{ - 1}^1 {S\left( x \right)dx} \).
c) Diện tích của mặt cắt là \(S\left( x \right) = 2\left( {1 - {x^2}} \right)\).
d) Thể tich của vật thể (T) bằng \(\frac{{16}}{3}\).
Cho hình phẳng được tô màu trong hình bên dưới
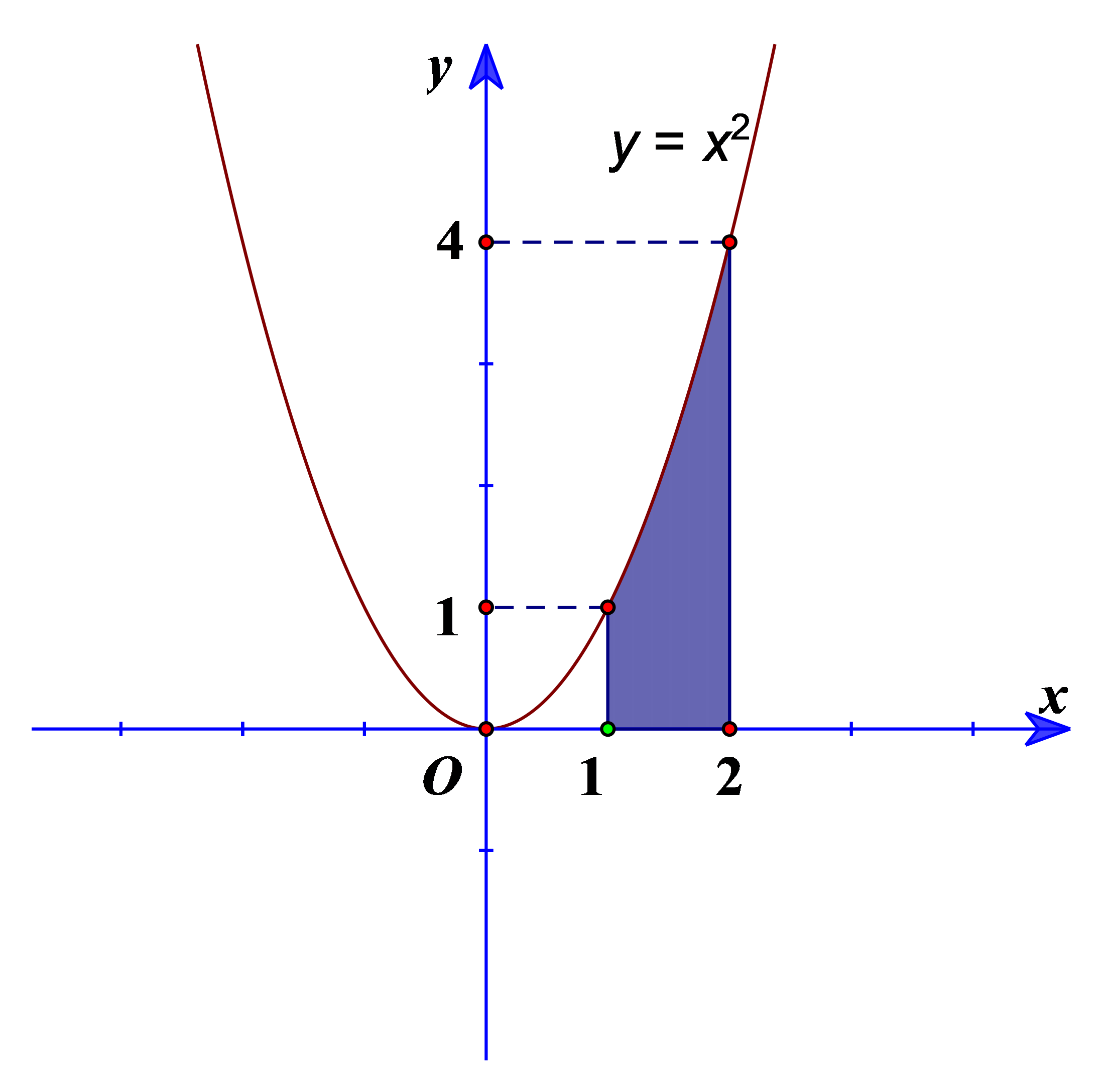
a) Hình phẳng được tô màu trong hình trên được giới hạn các đồ thị \(y = {x^2},y = 0,x = 1,x = 2\).
b) Diện tích hình phẳng phần tô màu trong hình vẽ là \(\int\limits_1^2 {{x^2}dx} \).
c) Hình phẳng được gạch chéo trong hình trên được giới hạn các đồ thị \(y = {x^2},y = 0,x = 0,x = 2\).
d) Diện tích hình phẳng gạch chéo trong hình vẽ bằng \(\frac{4}{3}\).
PHẦN III. TRẢ LỜI NGẮN
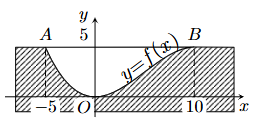
Biết diện tích phần tam giác cong OAB trong hình vẽ bên có diện tích là \(\frac{a}{b}\) với \(a,b \in \mathbb{Z}\) và phân số \(\frac{a}{b}\) tối giản.
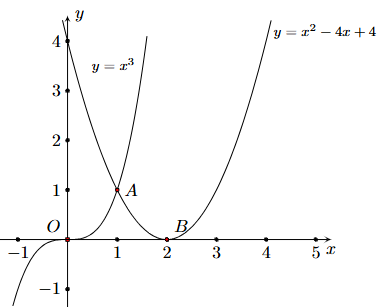
Tính hiệu \(b - a\).
Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục Ox (làm tròn đến hàng phần trăm).
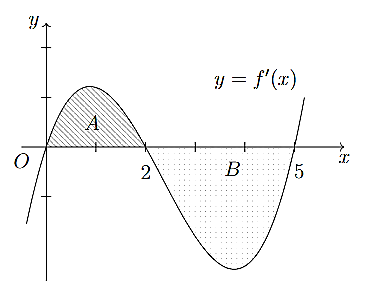
Cho hàm số \(y = f\left( x \right)\). Đồ thị của đạo hàm \(f'\left( x \right)\) là đường cong trong hình dưới. Biết rằng diện tích của các phần hình phẳng A và B lần lượt là SA = 2 và SB = 3. Cho f(0) = 4. Tính f(5).
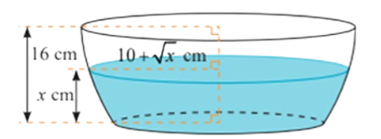
Nếu cắt chậu nước có hình dạng như hình vẽ bằng mặt phẳng song song và cách mặt đáy x (cm), (0 ≤ x ≤ 16) thì mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm). Tính dung tích của chậu (kết quả làm tròn đến hàng đơn vị của cm3).
Hình bên dưới minh họa mặt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong cho bởi phương trình \(y = f\left( x \right) = \frac{3}{{100}}\left( { - \frac{1}{3}{x^3} + 5{x^2}} \right)\). Biết đơn vị trên mỗi trục tọa độ là mét, diện tích mặt cắt đứng của mức nước trong con kênh là một phân số tối giản có dạng \(\frac{a}{b}\) m2, trong đó \(a,b \in \mathbb{N}*\). Tìm a.