20 câu trắc nghiệm Toán 12 Cánh diều Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Đồ thị hàm số nào dưới đây có dạng đường cong như hình vẽ?
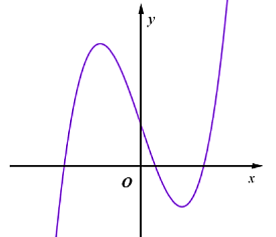
y = −x3 + 3x + 1.
B. 
.
y = x3 – 3x + 1.
D. 
.
Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
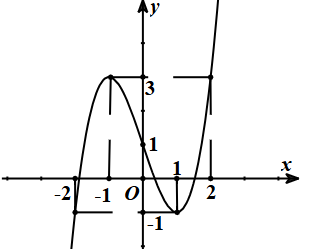
y = x3 − 3x + 1.
y = −x3 + 2x – 1.
y = 2x3 – 6x + 1.
y = −x3 + 3x + 1.
Hình vẽ bên dưới là đồ thị của hàm số nào
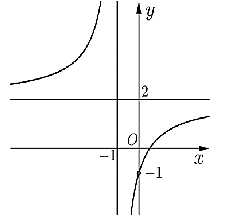
A. 
.
B. 
.
C. 
.
D. 
.
Bảng biến thiên sau là của hàm số nào dưới đây?
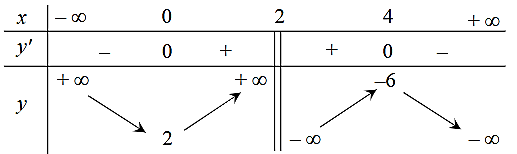
A. 
.
B. 
.
C. 
.
D. 
.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới
y = x2 – 2x + 2.
B. 
.
C. 
.
D. 
.
Hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ ℝ, a ≠ 0) có đồ thị như hình vẽ bên dưới
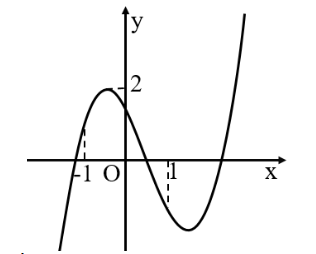
Trong các hệ số a, b, c, d có mấy hệ số mang giá trị dương.
2.
4.
1.
3.
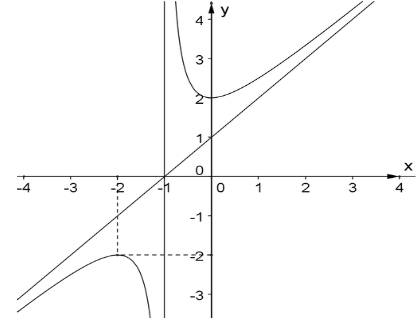
Cho hàm số 
(với a, b là các số thực, a ≠ 0; b ≠ 0) có đồ thị như hình vẽ
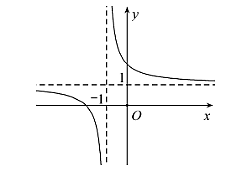
Khẳng định nào sau đây là đúng?
0 < a < b.
b < 0 < a.
a < b < 0.
0 < b < a.
Hãy xác định a, b để hàm số 
có đồ thị như hình vẽ
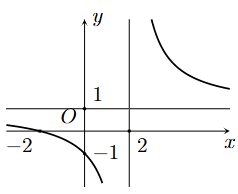
a = 1; b = −2.
a = b = 2.
a = −1; b = −2.
a = b = −2.
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình.
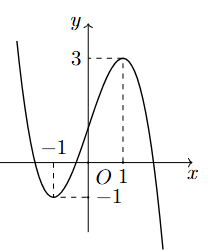
Số nghiệm thực của phương trình f(x) = 1 là:
0.
3.
1.
2.
Cho hàm số y = f(x) có bảng biến thiên như sau:
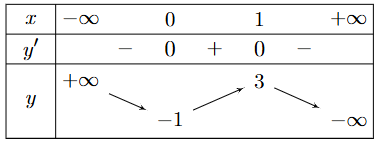
Số giao điểm của đồ thị hàm số y = f(x) với trục hoành là
0.
3.
1.
2.
a) Hàm số y = f(x) có hai điểm cực trị là x = 0 và x = 2
b) Giá trị b bằng 0.
c) Hàm số f(x) = x3 – 6x2 + 2.
d) Giá trị lớn nhất của hàm số f(x) trên đoạn [1; 4] là 30.
a) Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).
b) Hàm số nghịch biến trên ℝ.
c) Giá trị lớn nhất của hàm số y = f(x) trên đoạn [3; 4] là f(3).
d) Đồ thị (C) của hàm số y = f(x) là hình vẽ dưới
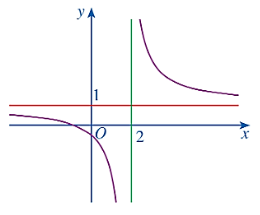
a) Đồ thị hàm số cắt trục hoành tại duy nhất một điểm
b) f(1) = 0.
c) ad > 0.
d) bc < 0.
a) Đồ thị hàm số có 1 đường tiệm cận đứng và 1 đường tiệm cận xiên.
b) Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt.
c) Hàm số có bảng biến thiên như sau:
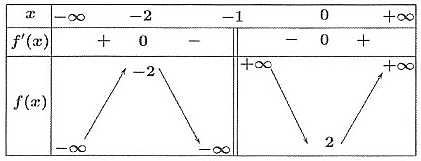
d) Trên (C) có đúng 3 điểm có tọa độ nguyên.
a) Đạo hàm của hàm số đã cho là 
.
b) Đạo hàm của hàm số đã cho nhận giá trị âm trên các khoảng (−2; 0) È (0; 2) và nhận giá trị dương trên các khảng (−∞; −2) È (2; +∞).
c) Bảng biến thiên của hàm số đã cho là
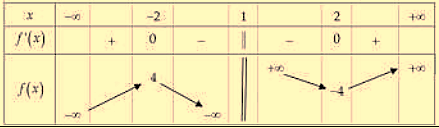
d) Đồ thị hàm số đã cho như hình
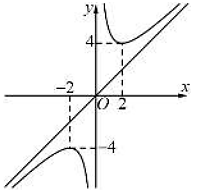
PHẦN III. TRẢ LỜI NGẮN
Cho hàm số 
có đồ thị như hình.
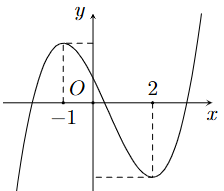
Tính giá trị của biểu thức T = 3[f(4) – f(0)].
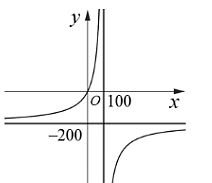
Để loại bỏ x% chất gây ô nhiễm môi trường từ khí thải của một nhà máy, người ta ước tính chi phí (triệu đồng) cần bỏ ra được mô hình hóa bởi hàm số có dạng 
, với 0 £ x £ 100 (như hình vẽ). Tính chi phí chênh lệch (tỉ đồng) phải bỏ ra để loại bỏ 90% và 99% chất gây ô nhiễm từ khí thải của nhà máy.
Dân số của một quốc gia sau t (năm) kể từ năm 2024 được ước tính bởi công thức N(t) = 100e0,012t (N(t) được tính bằng triệu người, 0 £ t £ 50). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm.
Biết đồ thị hàm số y = x3 + ax2 + bx + c đi qua điểm M(0; 2) và có điểm cực trị N(−4; 0). Tính giá trị của biểu thức 8a + b + c.
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:
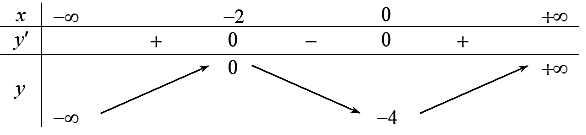
Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình f(x) = m – 1 có ba nghiệm thực phân biệt.
