20 câu trắc nghiệm Toán 12 Cánh diều Bài 3. Tích phân (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho \(f\left( x \right)\) liên tục trên \(\left[ {1;2} \right]\). Biết \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\) trên \(\left[ {1;2} \right]\) thỏa mãn \(F\left( 1 \right) = - 2,F\left( 2 \right) = 4\). Khi đó \(\int\limits_1^2 {f\left( x \right)dx} \) bằng
2.
6.
−2.
−6.
Nếu \(\int\limits_0^4 {f\left( x \right)dx} = 5\) và \(\int\limits_2^4 {f\left( x \right)dx} = - 1\) thì \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
−4.
6.
4.
−6.
Nếu \(\int\limits_1^4 {f\left( x \right)dx} = 3\) thì \(\int\limits_1^4 {\left[ {\frac{1}{3}f\left( x \right) - 5} \right]dx} \) bằng
−15.
−12.
−14.
−4.
Tích phân \(I = \int\limits_0^{2024} {{3^x}dx} \) bằng
\(\left( {{3^{2024}} - 1} \right)\ln 3\).
\(\frac{{{3^{2024}}}}{{\ln 3}}\).
\({3^{2024}} - 1\).
\(\frac{{{3^{2024}} - 1}}{{\ln 3}}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{{\sqrt[4]{{{x^3}}}}} + 2\;\;khi\;x \ge 1\\{x^2} + x + 1\;\;khi\;x < 1\end{array} \right.\). Biết tích phân \(\int\limits_{ - 1}^{16} {f\left( x \right)dx} = \frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản, b > 0). Tính tổng a + b.
120.
113.
90.
80.
Cho \(\int\limits_0^6 {f\left( x \right)dx} = 12\). Tính \(I = \int\limits_0^2 {f\left( {3x} \right)dx} \).
5.
36.
4.
6.
Giả sử f là hàm số liên tục trên khoảng K và a, b, c là các số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
\(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( t \right)dt} \).
\(\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)} dx = \int\limits_a^b {f\left( x \right)dx} \).
\(\int\limits_a^a {f\left( x \right)dx} = 1\).
\(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \).
Cho biết \(\int\limits_0^{\frac{\pi }{2}} {\left( {4 - \sin x} \right)dx} = a\pi + b\) với a, b là các số nguyên. Giá trị của biểu thức \(a + b\) bằng.
1.
−4.
6.
3.
Tính tích phân \(\int\limits_0^8 {\left| {{x^2} - 6x} \right|dx} \).
\(\frac{{152}}{3}\).
\(\frac{{64}}{3}\).
\(\frac{{ - 64}}{3}\).
\(\frac{{ - 152}}{3}\).
Một ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = 27 - 9\sqrt t \). Tính quãng đường mà ô tô di chuyển từ thời điểm \(t = 0\) đến thời điểm mà vật dừng lại.
\(120\) m.
\(18\) m.
\(81\) m.
\(54\) m.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho \(f\left( x \right),g\left( x \right)\) là hai hàm số liên tục trên đoạn \(\left[ { - 1;1} \right]\) và \(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số lẻ. Biết \(\int\limits_0^1 {f\left( x \right)dx} = 5,\int\limits_0^1 {g\left( x \right)dx} = 7\).
a) \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = 10\).
b) \(\int\limits_{ - 1}^1 {g\left( x \right)dx} = 14\).
c) \(\int\limits_{ - 1}^1 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = 10\).
d) \(\int\limits_{ - 1}^1 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = 10\).
Cho \(\int {f\left( x \right)dx} = {x^2} + x + {C_1},\int {g\left( x \right)dx} = {x^4} + {x^3} + {C_2}\).
a) \(f\left( x \right) = 2x + 1\).
b) \(g\left( 0 \right) = 1\).
c) \(\int\limits_0^1 {g\left( x \right)dx} = 3\).
d) \(\int\limits_0^1 {f\left( x \right)g\left( x \right)dx} = \frac{{51}}{{10}}\).
Sau khi xuất phát, ô tô di chuyển với tốc độ \(v\left( t \right) = 2,01t - 0,025{t^2}\left( {0 \le t \le 10} \right)\). Trong đó \(v\left( t \right)\) tính theo m/s, thời gian t tính bằng giây, t = 0 là thời điểm xe xuất phát.
a) Quãng đường xe di chuyển được tính theo công thức là \(s\left( t \right) = 2,01 - 0,05t\left( {0 \le t \le 10} \right)\).
b) Quãng đường xe di chuyển được trong 3 giây là 8,82 m.
c) Quãng đường xe di chuyển được trong giây thứ 9 xấp xỉ 15,277 m.
d) Trong khoảng thời gian không quá 10 giây đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe là 1,51 m/s2.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên
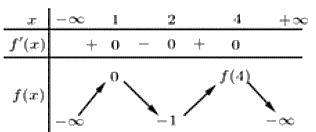
a) \(\int\limits_1^2 {f'\left( x \right)dx} = 1\).
b) \(\int\limits_1^4 {\left[ {3 + f'\left( x \right)} \right]dx} = f\left( 4 \right) + 3\).
c) \(\int\limits_1^2 {\left| {f'\left( x \right)} \right|dx} = f\left( 1 \right) - f\left( 2 \right)\).
d) Nếu \(\int\limits_1^4 {\left| {f'\left( x \right)} \right|dx} = 5\) thì \(f\left( 4 \right) = 3\).
Cho hàm số \(f\left( x \right) = \sin 2x\) liên tục trên ℝ, \(F\left( x \right)\) là nguyên hàm của \(f\left( x \right)\).
a) \(\int\limits_0^\pi {f\left( x \right)dx} = 0\).
b) Biết \(F\left( 0 \right) = \frac{1}{2}\) thì \(F\left( {\frac{\pi }{2}} \right) = 1\).
c) \(\int\limits_0^{\frac{\pi }{2}} {\left( {\cos x - f\left( x \right)} \right)dx} = 2\).
d) \(\int\limits_{ - \pi }^\pi {\left| {f\left( x \right)} \right|dx} = 4\).
PHẦN III. TRẢ LỜI NGẮN
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\). Giá trị của \(\int\limits_0^1 {\left( {2f\left( x \right) + {e^{2x}}} \right)dx} \) bằng \(\frac{{{e^a} + b}}{c}\). Khi đó \(a + b + c\) bằng bao nhiêu?
Cho \(\int\limits_0^1 {\frac{{xdx}}{{{{\left( {x + 2} \right)}^2}}}} = a + b\ln 2 + c\ln 3\) với a, b, c là các số hữu tỉ. Giá trị của 3a + b + c bằng bao nhiêu?
Cho các hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) liên tục trên \(\mathbb{R}\). Giả sử \(\int\limits_2^7 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]dx} = 2\) và \(\int\limits_2^7 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} = 4\). Khi đó \(\int\limits_2^7 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng bao nhiêu? (làm tròn kết quả đến chữ số thập phân thứ 2).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {0;2} \right]\). Giả sử \(y = F\left( x \right)\) là một nguyên hàm của \(y = f\left( x \right)\) và \(\int\limits_0^2 {f\left( x \right)dx} = 3\) và \(F\left( 0 \right) = 2\). Tính \(F\left( 2 \right)\).
Một chiếc máy bay chuyển động trên đường băng với vận tốc \(v\left( t \right) = {t^2} + 10t\) (m/s) với \(t\) là thời gian được tính bằng đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc 200 m/s thì nó rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị).

