20 câu trắc nghiệm Toán 12 Cánh diều Bài 3. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và\(\vec b\left( {1;2; - 1} \right)\). Tọa độ của vectơ \(\vec c = \vec a - \vec b\) là
\(\left( { - 1;0; - 2} \right)\).
\(\left( { - 2; - 2;4} \right)\).
\(\left( {2;2; - 4} \right)\).
\(\left( {0;2;2} \right)\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a = \left( {4; - 3; - 1} \right)\)và \(\overrightarrow b = \vec i + 2\vec j + \vec k\). Tìm tọa độ của \(2\vec a + 3\vec b\)
\(\left( {11;0;1} \right)\).
\(\left( {5; - 1;0} \right)\).
\(\left( {11;0; - 1} \right)\).
\(\left( {5; - 1; - 1} \right)\).
Trong không gian với hệ tọa độ \(Oxyz\), cho hai véc tơ \(\overrightarrow a \left( {2; - 1;3} \right)\) và \(\overrightarrow b \left( {1;3;2} \right)\). Khi đó tích vô hướng \(\overrightarrow a .\overrightarrow b \)bằng:
\( - 5\).
\(3\).
\(5\).
\( - 3\).
Trong không gian \(Oxyz\), cho 2 điểm \(A\left( {1;2;3} \right)\), \(B\left( { - 1;1; - 1} \right)\). Gọi \(I\) là trung điểm của đoạn thẳng \(AB\), tọa độ điểm \(I\) là
\(I\left( {0;\frac{3}{2}; - 1} \right)\).
\(I\left( {0;3;2} \right)\).
\(I\left( {2;\frac{5}{2};5} \right)\).
\(I\left( {0;\frac{3}{2};1} \right)\).
Trong không gian\(Oxyz\), cho tam giác \(\Delta ABC\) có \(A\left( {1; - 1;2} \right)\), \(B\left( {2; - 1;3} \right)\), \(C\left( {2;3;1} \right)\). Gọi \(G\)là trọng tâm tam giác \(\Delta ABC\), tọa độ điểm \(G\) là
\(G\left( {\frac{5}{3};\frac{1}{3}; - 2} \right)\).
\(G\left( {\frac{5}{2};\frac{1}{2};3} \right)\).
\(G\left( {5;1;6} \right)\).
\(G\left( {\frac{5}{3};\frac{1}{3};2} \right)\).
Trong không gian \(Oxyz\), cho hai điểm \(A\left( {1;{\rm{ }} - 1;{\rm{ }}2} \right)\) và \(B\left( {2;{\rm{ }}1;{\rm{ }}1} \right)\). Độ dài đoạn thẳng\(AB\) bằng
\(2\).
\(\sqrt 6 \).
\(\sqrt 2 \).
\(6\).
Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và\(\vec b\left( {1;2; - 1} \right)\). Vectơ vuông góc với cả hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)là
\(\vec c\left( { - 6; - 2; - 2} \right)\).
\(\vec d\left( {3; - 1;1} \right)\).
\(\vec m\left( { - 3; - 1;1} \right)\).
\(\vec n\left( {2;1;4} \right)\).
Trong không gian tọa độ Oxyz cho ba điểm A(−1; −2; 3), B(0; 3; 1), C(4; 2; 2). Cosin của góc \(\widehat {BAC}\) là
\(\frac{9}{{\sqrt {35} }}\) .
\( - \frac{9}{{\sqrt {35} }}\).
\( - \frac{9}{{2\sqrt {35} }}\).
\(\frac{9}{{2\sqrt {35} }}\).
Trong không gian \[Oxyz\], cho hai điểm \(A\left( {4;\,\,2;\,\,1} \right)\), \(B\left( { - 2;\, - 1;\,4} \right)\). Tìm tọa độ điểm \(M\)thỏa mãn đẳng thức \(\overrightarrow {AM} = 2\overrightarrow {MB} \).
\(M(0;0; - 3)\).
\(M( - 8; - 4;7)\).
\(M(8;{\mkern 1mu} {\mkern 1mu} 4; - 7)\).
\(M\left( {0;0;3} \right)\).
Trong không gian với hệ tọa độ \[Oxyz\] cho ba điểm \(M\left( {2;\,3;\, - 1} \right)\), \(N\left( { - 1;1;1} \right)\) và \(P\left( {1;m - 1;\,2} \right)\). Tìm \(m\) để tam giác \(MNP\) vuông tại \(N\).
m = 2
m = −6
m = 0.
m = −4.
Trong không gian Oxyz cho hai điểm M(2; 3; −1), N(−1; 1; 1).
(a) Độ dài của vectơ \(\overrightarrow {MN} \) bằng \(\sqrt {17} \).
(b) Cho P(1; m – 1; 3). Tam giác MNP vuông tại N khi và chỉ khi m = 1.
(c) Tọa độ vectơ \(\overrightarrow {OM} = 2\overrightarrow i - 3\overrightarrow j + \overrightarrow k \).
(d) Tọa độ vectơ \(\overrightarrow v = \overrightarrow {OM} + \overrightarrow {ON} \) là \(\overrightarrow v = \left( {1;4;0} \right)\).
Trong không gian Oxyz, cho ba điểm A(1; 2; −1), B(2; −1; 3), C(−4; 7; 5).
(a) Tọa độ trọng tâm tam giác ABC là \(G\left( { - \frac{1}{3};\frac{8}{3};\frac{7}{3}} \right)\).
(b) ABCD là hình bình hành với điểm D(2; 1; −3).
(c) Điểm M(x; y; z) thỏa mãn \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \) thì ta có 4x + 4y + z = 10.
(d) \(\overrightarrow {AB} .\overrightarrow {AC} = - 5\).
Trong không gian Oxyz, cho ba điểm A(−1; 2; 0), B(2; −5; 4), C(0; 2; 0).
(a) \(\overrightarrow {AB} - 3\overrightarrow {AC} = \left( {6; - 7;4} \right)\).
(b) Vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương.
(c) Điểm M(a; b; c) thuộc mặt phẳng (Oyz) để biểu thức \(T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất. Khi đó \(a + b + c = \frac{5}{3}\).
(d) Chu vi tam giác ABC bằng \(1 + \sqrt {74} + \sqrt {69} \).
Trong không gian tọa độ Oxyz cho hai điểm A(2; 2; 1), \(B\left( { - \frac{8}{3};\frac{4}{3};\frac{8}{3}} \right)\).
(a) Độ dài đoạn thẳng \(AB = \sqrt 5 \).
(b) Tam giác OAB là tam giác nhọn.
(c) Chân đường phân giác trong góc \(\widehat {AOB}\) là \(D\left( {0;\frac{{12}}{7};\frac{{12}}{7}} \right)\).
(d) Biết I(a; b; c) là tâm đường tròn nội tiếp của tam giác OAB. Khi đó S = a + b + c = 2.
Hình vẽ sau mô tả vị trí của máy bay vào thời điểm 9h30 phút. Biết các đơn vị trên hình tính theo đơn vị km.
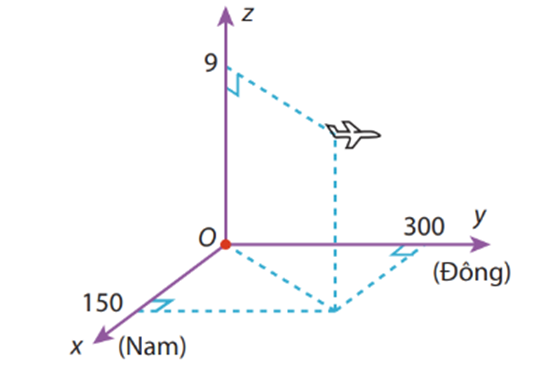
(a) Máy bay đang ở độ cao 9 km.
(b) Tọa độ của máy bay (300; 150; 9).
(c) Phi công để máy bay ở chế độ tự động với vận tốc theo hương đông là 750 km/h, độ cao không đổi. Biết rằng gió thổi theo hướng đông với vận tốc 10 m/s. Giả sử vận tốc và hướng gió không đổi thì lúc 10 giờ 30 phút máy bay ở tọa độ (150; 1086; 9).
(d) Sau khi bay đến vị trí lúc 10 giờ 30 phút thì máy bay bay ngược lại với vận tốc 800 km/h với độ cao không đổi, biết lúc đó trời lặng gió thì lúc 11 giờ máy bay ở tọa độ (686; 150; 9).
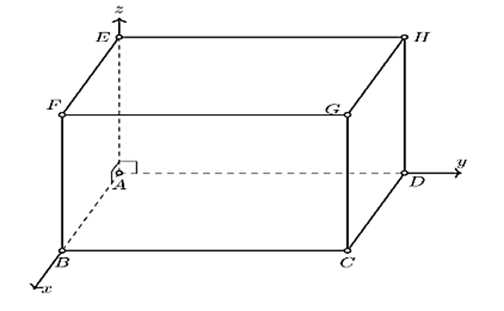
Cho hình hộp ABCD.EFGH có AB = 6; AD = 7; AE = 5. Xét hệ trục tọa độ Oxyz có gốc O trùng với điểm A, các điểm B, D, E lần lượt nằm trên các tia Ox, Oy, Oz. Gọi K là tâm của ABCD. Điểm N(a; b; c) là trọng tâm của tam giác AHK. Tính P = 2a – 4b + 3c.
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí A cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m (hình vẽ). Để thực hiện nhiệm vụ tiếp theo, người điều khiển flycam đến vị trí B cách vị trí điều khiển 80 m về phía bắc và 120 m về phía tây, đồng thời cách mặt đất 50 m.
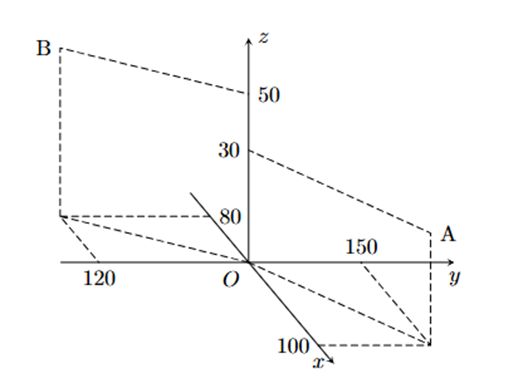
Chọn hệ trục tọa độ Oxyz với gốc O là vị trí người điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox có hướng trùng với hướng nam, trục Oy có hướng trùng với hướng đông, trục Oz vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên các trục tương ứng với 1 m. Tính quãng đường flycam bay từ vị trí A đến vị trí B, biết flycam bay từ vị trí A đến vị trí B theo một đường thẳng (làm tròn kết quả đến hàng đơn vị của mét).
Trong không gian Oxyz, cho hai điểm A(1; 3; 1), B(1; −2; 3). Biết điểm M(x; 0; z) thuộc mặt phẳng tọa độ (Oxz) sao cho MA + MB ngắn nhất. Tính giá trị của biểu thức P = 3z – x2.
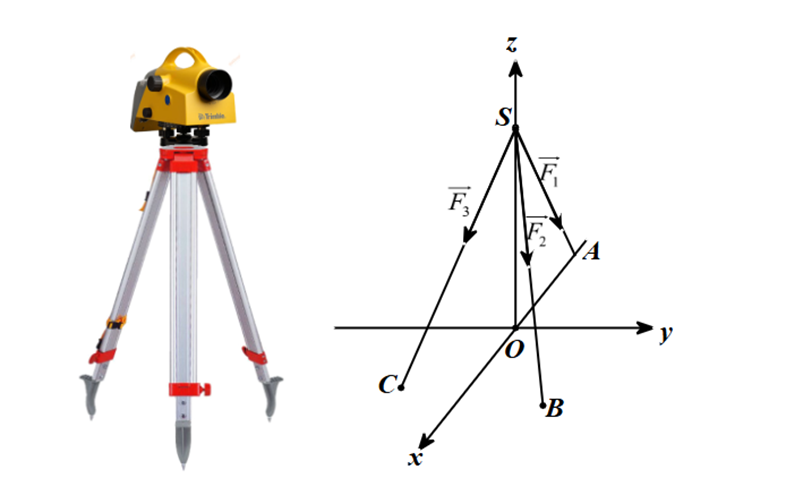
Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân với điểm đặt S(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \(A\left( { - 2;0;0} \right),B\left( {1;\sqrt 3 ;0} \right),C\left( {1; - \sqrt 3 ;0} \right)\). Biết rằng trọng lực tác dụng lên chiếc máy có độ lớn 30 N và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) có độ lớn bằng nhau như hình. Tính tích vô hướng của \(\overrightarrow {{F_1}} .\overrightarrow {{F_2}} \).
Trong phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một drone giao hàng đang ở tọa độ A(1; 0; 1) di chuyển đến địa điểm nhận hàng là B(4; 4; 6). Mỗi đơn vị trên phần mềm bằng 1 km ngoài thực tế. Biết tốc độ của drone là 80 km/h. Giả sử rằng từ vị trí giao hàng và nhận hàng không gặp chướng ngại vật, sức cản gió khống đáng kể để drone bay theo đường thẳng. Thời gian drone bay từ vị trí ban đến đến địa điểm giao hàng mất bao nhiêu phút (làm tròn đến hàng phần mười).

