20 câu trắc nghiệm Toán 12 Cánh diều Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
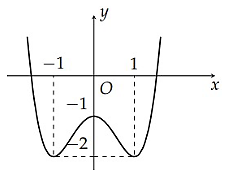
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) trên [−1; 1]. Khẳng định nào sau đây là đúng?
m + M = 2.
m + M = −2.
m + M = −3.
m + M = 0.
Cho hàm số f(x) liên tục trên đoạn [−2; 2] có đồ thị như hình vẽ
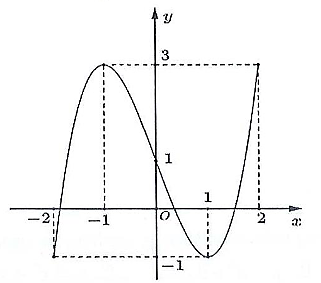
Giá trị nhỏ nhất của hàm số trên đoạn [−2; 2] là
1.
−1.
−2.
3.
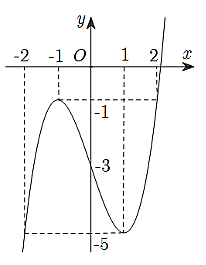
Cho hàm số y = f(x) xác định và liên tục trên ℝ có đồ thị như hình vẽ. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn [−2; 2].
m = −5; M = −1.
m = −5; M = 0.
m = −2; M =2.
m = −1; M = 0.
Cho hàm số y = f(x) liên tục trên [−3; 2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [−1; 2]. Tính M + m.
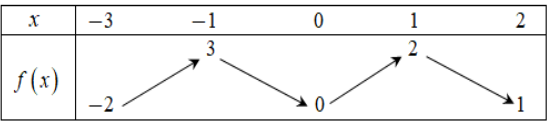
4.
1.
3.
2.
Cho bảng biến thiên của hàm số y = f(x). Giá trị nhỏ nhất của hàm số trên đoạn [−1; 1] là:
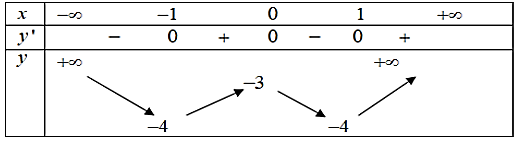
0.
−1.
−4.
−3.
Cho hàm số y = f(x) liên tục trên ℝ, có bảng biến thiên như sau:
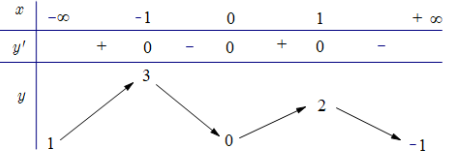
Giá trị lớn nhất của hàm số trên (−∞; 1) là
2.
1.
0.
3.
Giá trị nhỏ nhất của hàm số y = x3 + 6x2 – 3 trên đoạn [−2; 2] là
29.
13.
−3.
−4.
Giá trị lớn nhất của hàm số 
trên đoạn [−1; 0] là
3.
−3.
4.
−4.
Giá trị lớn nhất của hàm số y = −x3 + 3x + 1 trên khoảng (0; +∞) bằng
−1.
0.
2.
3.
Tìm giá trị nhỏ nhất của hàm số y = (x2 – 9x + 15)ex trên đoạn [0; 9].
25e10.
15e9.
C. 
.
D. 
.
a) Để đạt lợi nhuận lớn nhất thì mỗi bánh xà phòng cần tăng thêm 20000 đồng.
b) Để đạt lợi nhuận lớn nhất thì mỗi bánh xà phòng cần bán với giá 49000 đồng.
c) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi bánh xà phòng lãi 31000 đồng.
d) Để đạt lợi nhuận lớn nhất thì số bánh xà phòng bán ra giảm 2000 bánh.
a) Hàm số đã cho nghịch biến trên các khoảng (−∞; 1) và (1; 2).
b) Hàm số đã cho có 2 điểm cực trị.
c) Trên đoạn [−1; 1], giá trị lớn nhất của hàm số đã cho bằng 2.
d) Trên đoạn [1; 3], giá trị nhỏ nhất của hàm số đã cho bằng −2.
a) Giá trị lớn nhất của hàm số trên ℝ bằng 21.
b) Giá trị nhỏ nhất của hàm số trên ℝ bằng 12
c) Giá trị lớn nhất của hàm số h(x) = f(x) + m trên đoạn [0; 5] bằng 34 khi m = 15.
d) Hàm số g(x) = f(2x – 2) đạt giá trị lớn nhất trên khoảng (−∞; 4) tại x = 3.
a) Giả sử trong một ngày nào đó cơ sở sản xuất được 10 đôi giầy thì lợi nhuận thu được là 1888.
b) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là 1584 khi đó cơ sở phản sản xuất được 9 đôi giầy.
c) Cơ sở này sản xuất được 12 đôi giầy thì lợi nhuận thu được là nhiều nhất.
d) Lợi nhuận tối đa thu được trong một ngày là 1980 nghìn đồng
a) Tập xác định của hàm số là D = [−1; 1].
b) $y' = \frac{{\sqrt {1 - x} - \sqrt {1 + x} }}{{2\sqrt {1 - {x^2}} }}\forall x \in \left( { - 1;1} \right)$ .
c) 
.
d) 
.
PHẦN II. TRẢ LỜI NGẮN
Người ta giới thiệu một loại thuốc để kích thích sự sinh sản của một loại vi khuẩn. Sau t phút số vi khuẩn được xác định theo công thức f(t) = −t3 + 15t2 + 100 với 0 ≤ t ≤ 15. Hỏi số vi khuẩn lớn nhất bằng bao nhiêu?
Cho hàm số y = x – lnx. Giá trị lớn nhất của hàm số trên đoạn 
có dạng a + be với a, b Î ℤ. Tính 2a + b.
Một hộ sản xuất kinh doanh hạt điều sấy mỗi ngày sản xuất được x kg (5 £ x £ 20). Tổng chi phí sản xuất x kg được cho bởi hàm chi phí C(x) = x3 – 3x2 + 19x + 300 (đơn vị: nghìn đồng). Giả sử hộ sản xuất này bán hết sản phẩm mỗi ngày với giá 316 nghìn đồng/kg. Hỏi hộ sản xuất này cần sản xuất và bán ra mỗi ngày bao nhiêu kg hạt điều để thu được lợi nhuận lớn nhất?
Biết giá trị nhỏ nhất của hàm số 
trên đoạn [1; 4] bằng 
. Tính giá trị a + 2b.
Hằng ngày, mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các suối nước đổ về hồ. Từ lúc 8 giờ sáng, độ sâu của mực nước trong hồ (tính theo mét) và lên xuống theo thời gian t (giờ) trong ngày được cho bởi công thức 
. Biết phải thông báo cho các hộ dân phải di dời đi trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước mấy giờ? Biết rằng mực nước trong hồ phải dâng lên cao nhất mới xả nước.
