10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ. Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số f(x) trên [−1; 1]. Khẳng định nào sau đây là đúng?
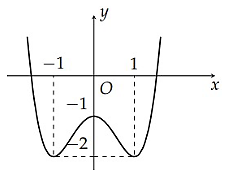
m + M = 2.
m + M = −2.
m + M = −3.
m + M = 0.
Cho hàm số f(x) liên tục trên đoạn [−2; 2] có đồ thị như hình vẽ
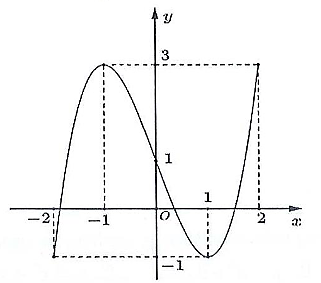
Giá trị nhỏ nhất của hàm số trên đoạn [−2; 2] là
1.
−1.
−2.
3.
Cho hàm số y = f(x) xác định và liên tục trên ℝ có đồ thị như hình vẽ. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn [−2; 2].
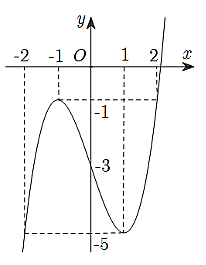
m = −5; M = −1.
m = −5; M = 0.
m = −2; M =2.
m = −1; M = 0.
Cho hàm số y = f(x) liên tục trên [−3; 2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [−1; 2]. Tính M + m.
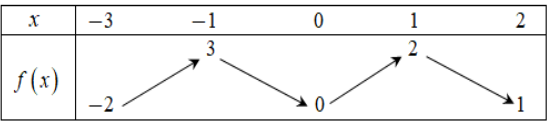
4.
1.
3.
2.
Cho bảng biến thiên của hàm số y = f(x). Giá trị nhỏ nhất của hàm số trên đoạn [−1; 1] là:
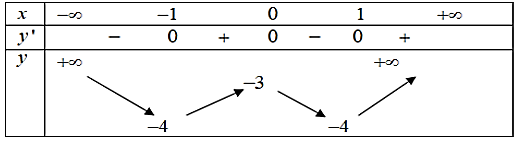
0.
−1.
−4.
−3.
Cho hàm số y = f(x) liên tục trên ℝ, có bảng biến thiên như sau:
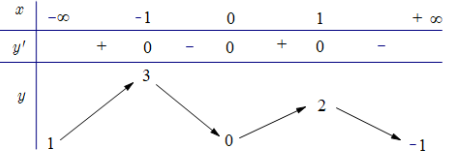
Giá trị lớn nhất của hàm số trên (−∞; 1) là
2.
1.
0.
3.
Giá trị nhỏ nhất của hàm số y = x3 + 6x2 – 3 trên đoạn [−2; 2] là
29.
13.
−3.
−4.
Giá trị lớn nhất của hàm số ![]() trên đoạn [−1; 0] là
trên đoạn [−1; 0] là
3.
−3.
4.
−4.
Giá trị lớn nhất của hàm số y = −x3 + 3x + 1 trên khoảng (0; +∞) bằng
−1.
0.
2.
3.
Tìm giá trị nhỏ nhất của hàm số y = (x2 – 9x + 15)ex trên đoạn [0; 9].
25e10.
15e9.
C. ![]() .
.
D. ![]() .
.
