10 câu hỏi
Cho hình lập phương ABCD.A'B'C'D'. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương ABCD.A'B'C'D' và bằng vectơ \(\overrightarrow {AD} \) là
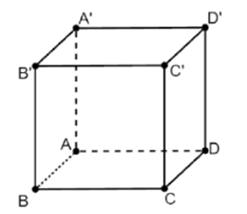
\(\overrightarrow {B'C'} \).
\(\overrightarrow {DA} \).
\(\overrightarrow {CB} \).
\(\overrightarrow {AB} \).
Trong không gian, cho 3 điểm A, B, C phân biệt. Hiệu hai vectơ \(\overrightarrow {AB} - \overrightarrow {AC} \) bằng
\(\overrightarrow {CB} \).
\(\overrightarrow {BC} \).
\(\overrightarrow {BA} \).
\(\overrightarrow {CA} \).
Cho hình hộp chữ nhật ABCD.A'B'C'D' (tham khảo hình vẽ dưới). Khẳng định nào dưới đây đúng?
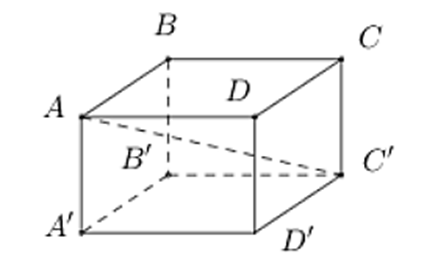
\(\overrightarrow {AC'} = \overrightarrow {BD'} \).
\(\overrightarrow {AD} \) cùng hướng với \(\overrightarrow {B'C'} \).
\(\overrightarrow {CD} \) cùng hướng với \(\overrightarrow {D'C'} \).
\(\overrightarrow {AC'} \) cùng phương với \(\overrightarrow {A'C'} \).
Cho hình lăng trụ tam giác ABC.A'B'C'. Vectơ \(\overrightarrow {AC} - \overrightarrow {AA'} - \overrightarrow {AB} \) bằng vectơ nào sau đây?
\(\overrightarrow {B'C} \).
\(\overrightarrow {BC'} \).
\(\overrightarrow {AB} \).
\(\overrightarrow {AC'} \).
Cho tứ diện ABCD. Gọi M là trung điểm của BC. Trong các khẳng định sau, khẳng định nào đúng?
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} - 2\overrightarrow {AD} } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( { - 2\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow {AB} - 2\overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {DM} = \frac{1}{2}\left( {\overrightarrow {AB} + 2\overrightarrow {AC} - \overrightarrow {AD} } \right)\).
Cho hình hộp ABCD.MNPQ. Gọi I, J lần lượt là trung điểm của AN và CQ. Khẳng định nào dưới đây đúng?
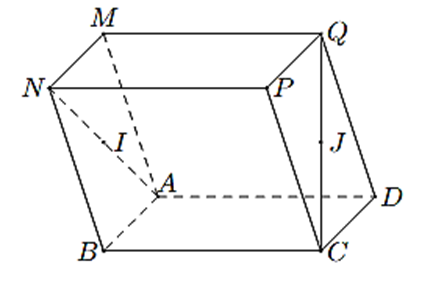
\(\overrightarrow {MI} = \overrightarrow {JC} \).
\(\overrightarrow {AI} = \overrightarrow {CJ} \).
\(\overrightarrow {QM} = \overrightarrow {IJ} \).
\(\overrightarrow {BI} = \overrightarrow {QJ} \).
Cho hình chóp S.ABC có ba cạnh SA, SB, SC đôi một vuông góc. Góc tạo bởi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {SB} \) bằng
120°.
60°.
90°.
45°.
Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, SB. Khi đó số đo góc giữa hai vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {CB} \) bằng với số đo của góc nào sau đây?
\(\widehat {PMN}\).
\(\widehat {MNP}\).
\(\widehat {MPN}\).
\(\widehat {ASB}\).
Cho tứ diện đều ABCD cạnh a. Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) theo a.
\(\frac{1}{2}{a^2}\).
2.
−a2.
\(\frac{{{a^2}\sqrt 3 }}{2}\).
Cho tứ diện đều ABCD có cạnh bằng 1. Tích vô hướng \(\overrightarrow {AB} \left( {4\overrightarrow {BC} + 3\overrightarrow {CD} } \right)\) bằng
1.
0.
−1.
−2.
