20 câu trắc nghiệm Toán 12 Cánh diều Bài 1: Phương trình mặt phẳng (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Trong không gian Oxyz, cho mặt phẳng \(\left( \alpha \right):x + 2y + z - 5 = 0\) và các vectơ sau: \(\overrightarrow a = \left( {1;2;1} \right),\overrightarrow b = \left( { - 1; - 2; - 1} \right),\overrightarrow c = \left( {2;1; - 5} \right),\overrightarrow d = \left( {1;1;2} \right),\overrightarrow e = \left( { - 5; - 10; - 5} \right)\). Có bao nhiêu vectơ là vectơ chỉ phương của mặt phẳng (α)?
\(1\).
\(2\).
\(3\).
\(4\).
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng \(\frac{x}{{ - 2}} + \frac{y}{{ - 1}} + \frac{z}{3} = 1\) là
\(\overrightarrow n = \left( {3;6; - 2} \right)\).
\(\overrightarrow n = \left( {2; - 1;3} \right)\).
\(\overrightarrow n = \left( { - 3; - 6; - 2} \right)\).
\(\overrightarrow n = \left( { - 2; - 1;3} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left( \alpha \right):x + y + z - 6 = 0\). Điểm nào dưới đây không thuộc (α).
\(Q\left( {3;3;0} \right)\).
\(N\left( {2;2;2} \right)\).
\(P\left( {1;2;3} \right)\).
\(M\left( {1; - 1;1} \right)\).
Trong không gian Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm \(M\left( {1;2; - 3} \right)\) và có một vectơ pháp tuyến \(\overrightarrow n = \left( {1; - 2;3} \right)\).
\(x - 2y + 3z + 12 = 0\).
\(x - 2y - 3z - 6 = 0\).
\(x - 2y + 3z - 12 = 0\).
\(x - 2y - 3z + 6 = 0\).
Trong không gian Oxyz, khoảng cách từ M(1; 2; −3) đến (P): x + 2y + 2z – 10 = 0 là
\(3\).
\(\frac{2}{3}\).
\(\frac{4}{3}\).
\(\frac{{11}}{3}\).
Trong không gian Oxyz, cho ba điểm \(A\left( {3; - 2; - 2} \right),B\left( {3;2;0} \right),C\left( {0;2;1} \right)\). Phương tình mặt phẳng (ABC) là
\(2x - 3y + 6z + 12 = 0\).
\(2x + 3y - 6z - 12 = 0\).
\(2x - 3y + 6z = 0\).
\(2x + 3y + 6z + 12 = 0\).
Trong không gian Oxyz, cho hai điểm A(2; 4; 1), B(−1; 1; 3) và mặt phẳng (P): x – 3y + 2z – 5 = 0. Lập phương trình mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P).
\(2y + 3z - 11 = 0\).
\(2x - 3y - 11 = 0\).
\(x - 2y + 2z - 5 = 0\).
\(3y + 2z - 11 = 0\).
Trong không gian Oxyz, cho hai điểm A(1; 2; 3) và B(1; −4; 1). Mặt phẳng đi qua A và vuông góc với đường thẳng AB có phương trình là
\( - 6y - 2z - 18 = 0\).
\(3y + z + 1 = 0\).
\( - 6y - 2z - 22 = 0\).
\(3y + z - 9 = 0\).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(3; −1; −2) và mặt phẳng (α): \(3x - y + 2z + 4 = 0\). Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với (α)?
\(3x + y - 2z - 14 = 0\).
\(3x - y - 2z + 6 = 0\).
\(3x - y + 2z - 6 = 0\).
\(3x - y - 2z + 6 = 0\).
Cho mặt phẳng \(\left( \alpha \right):2x + y - 3z + 8 = 0\). Mặt phẳng nào sau đây vuông góc với mặt phẳng (α)?
\(x - 3y + 3z - 7 = 0\).
\(3x - 3y + z - 7 = 0\).
\(x + 2y - z - 8 = 0\).
\(x - 2y + z + 8 = 0\).
Trong không gian Oxyz, cho mặt phẳng (P): \(2z - 3y + x - 4 = 0\).
(a) Một vectơ pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = \left( { - 1;3; - 2} \right)\).
(b) Điểm \(M\left( { - 3;3;8} \right)\) thuộc mặt phẳng (P).
(c) Khoảng cách từ điểm N(1; 0; 9) đến mặt phẳng (P) bằng \(\frac{{\sqrt {14} }}{2}\).
( d) Gọi (Q) là mặt phẳng qua A(1; 2; −3) và song song với (P). Khi đó \(\left( Q \right):x - 3y + 2z + 1 = 0\).
Trong không gian Oxyz, cho hai điểm A(1; 0; 0), B(4; 1; 2).
(a) \(\overrightarrow {AB} = \left( {3;1;2} \right)\).
(b) Mặt phẳng đi qua A và vuông góc với AB có phương trình là \(3x + y + 2z - 3 = 0\).
(c) Nếu I là trung điểm đoạn thẳng AB thì \(I\left( {\frac{5}{2};\frac{1}{2};1} \right)\).
(d) Mặt phẳng trung trực đoạn thẳng AB có phương trình là \(3x + y + 2z - 12 = 0\).
a) Trong không gian Oxyz, cho \(M\left( { - 2; - 4;3} \right)\) và \(\left( P \right):2x - y + 2z - 3 = 0\), \(\left( Q \right):2x - y + 2z - 6 = 0\).
( a) \(d\left( {M,\left( P \right)} \right) = 2\).
(b) M cách đều hai mặt phẳng (P) và (Q).
(c) \(d\left( {\left( P \right),\left( Q \right)} \right) = 1\).
(d) (α) song song và cách (Q) một khoảng bằng 2 có phương trình là \(\left( \alpha \right):2x - y + 2z - 9 = 0\).
Trong không gian Oxyz, cho A(3; 9; −1), B(2; 0; 1) và hai mặt phẳng (P): \(x - 2y + 2z - 3 = 0\), \(\left( Q \right):2x - 4y + 4z + 7 = 0\).
( a) (P) song song với (Q).
(b) Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 10.
(c) Điểm C thuộc mặt phẳng (P) và thẳng hàng với A, B có tọa độ là \(C\left( {\frac{{43}}{{21}};\frac{3}{7};\frac{{19}}{{21}}} \right)\).
(d) Phương trình mặt phẳng (β) đi qua điểm B và vuông góc với hai mặt phẳng (P) và mặt phẳng (Oxy) là \(x + y + z - 1 = 0\).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – 2y + z + 3 = 0 và điểm A(1; −2; 3). Khi đó:
(a) d(A, (P)) = 4.
(b) (P) cắt trục Ox tại điểm có hoành độ bằng 1.
(c) (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 2;1} \right)\).
(d) Gọi M(a; b; c) (P) thỏa mãn AM = 4 thì \(a + b + c = \frac{2}{3}\).
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 1; −1) và mặt phẳng (P): \(ax - 3y - z - 8 = 0\) (với a là hằng số). Biết rằng mặt phẳng (P) đi qua điểm M. Giá trị của a bằng bao nhiêu?
Trong không gian Oxyz, một ngôi nhà như hình vẽ dưới đây có sàn nhà nằm trên mặt phẳng (Oxy). Hai mái nhà lần lượt nằm trên các mặt phẳng (P): \(x - 2y + 5 = 0\) và \(\left( Q \right):x - 2y - 3z + 20 = 0\). Hỏi là chiều cao của ngôi nhà tính từ sàn nhà lên nóc nhà là bao nhiêu? (làm tròn đến hàng đơn vị).

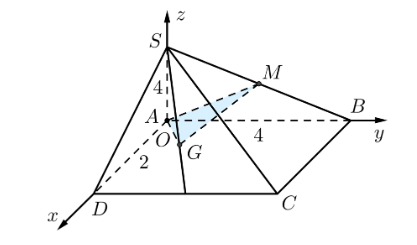
Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Biết A(0; 0; 0), D(2; 0; 0), B(0; 4; 0), S(0; 0; 4). Gọi M là trung điểm của SB và G là trọng tâm của tam giác SCD. Tính khoảng cách từ điểm B đến mặt phẳng (AMG) (kết quả làm tròn đến hàng phần trăm).
Cho điểm M(1; 3; 4). Gọi A, B, C lần lượt là hình chiếu của M lên các trục Ox, Oy, Oz. Mặt phẳng (ABC) có một vectơ pháp tuyến là \(\overrightarrow n = \left( {a;4;b} \right)\). Tính \(2a + b\).
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2; 0; 0), B(0; 4; 0), C(0; 0; −2) và \(D\left( {2;1;3} \right)\). Độ dài đường cao của tứ diện ABCD vẽ từ đỉnh D bằng \(\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính \(T = a - 2b\).

