10 câu hỏi
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả khảo sát được ghi lại ở bảng sau:
|
Mức giá (triệu đồng/m2) |
[10;14) |
[14;18) |
[18;22) |
[22;26) |
[26;30) |
|
Số khách hàng |
54 |
78 |
120 |
45 |
12 |
Khoảng biến thiên \(R\) của mẫu số liệu ghép nhóm trên là.
\(R = 4\).
\(R = 20\).
\(R = 9\).
\(R = 108\).
Gọi \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của một mẫu số liệu ghép nhóm. Khi đó khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu trên được xác định bởi công thức
\[{\Delta _Q}\; = {Q_2} - {Q_1}\].
\[{\Delta _Q}\; = {Q_3} - {Q_1}\].
\[{\Delta _Q}\; = {Q_2} - {Q_3}\].
\[{\Delta _Q}\; = {Q_1} - {Q_3}\].
Biểu diễn mẫu số liệu ghép nhóm về cân nặng (đơn vị: kilogam) của 40 học sinh một lớp 12 ở một trường trung học phổ thông được cho dưới bảng sau.
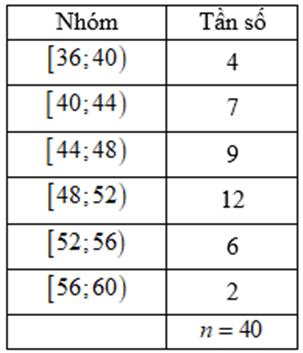
Khoảng biến thiên của mẫu số liệu ghép nhóm đó là
\(24\).
\(4\).
\(12\).
\(6\).
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau.
|
Tuổi thọ |
[2;3,5) |
[3,5;5) |
[5;6,5) |
[6,5;8) |
|
Số bóng đèn |
8 |
22 |
35 |
15 |
Khoảng biến thiên của mẫu số liệu trên là
\(3\).
\(6\)
\(5,5\).
\(4,5\).
Một cuộc khảo sát đã tiến hành xác định tuổi (theo năm) của 120 chiếc ô tô. Kết quả điểu tra được cho trong bảng sau.
|
Số tuổi (theo năm) |
[0; 4) |
[4; 8) |
[8; 12) |
[12; 16) |
[20; 24) |
|
Số ô tô |
23 |
25 |
37 |
26 |
19 |
Khoảng biến thiên của mẫu số liệu trên là
\(16\).
\(20\)
\(24\).
\(4\).
Số lượng đặt bàn của một nhà hàng được cho bởi bảng sau:
|
Số lượt đặt bàn |
Tần số |
Tần số tích lũy |
|
[1; 6) |
14 |
14 |
|
[6; 11) |
30 |
44 |
|
[11; 16) |
25 |
69 |
|
[16; 21) |
18 |
87 |
|
[21; 26) |
5 |
92 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi bảng trên.
\({\Delta _Q} = \frac{{11}}{6}\).
\[{\Delta _Q}\; = \frac{{17}}{2}\].
\({\Delta _Q} = \frac{5}{2}\).
\({\Delta _Q} = \frac{{17}}{6}\).
Giả sử kết quả khảo sát khu vực A về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:
|
Tuổi kết hôn |
Tần số |
Tần số tích lũy |
|
[19; 22) |
10 |
10 |
|
[22; 25) |
27 |
37 |
|
[25; 28) |
31 |
68 |
|
[28; 31) |
25 |
93 |
|
[31; 34) |
7 |
100 |
Hãy tính khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu trên.
\[{\Delta _Q} = \frac{{388}}{{75}}\].
\[{\Delta _Q} = \frac{{378}}{{75}}\].
\[{\Delta _Q} = \frac{{386}}{{75}}\].
\[{\Delta _Q} = \frac{{288}}{{75}}\].
Cho mẫu số liệu ghép nhóm về độ tuổi của dân cư của khu phố \(A\) như sau

Khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là (làm tròn đến hàng phần trăm).
\(30,38\).
\(53,33\).
\(22,95\).
\(22,94\).
Bảng sau thống kê cân nặng của 30 quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan
|
Cân nặng (g) |
[750;800) |
[800;850) |
[850;900) |
[900;950) |
[950;1000) |
|
Số quả bưởi |
5 |
10 |
5 |
8 |
2 |
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
\(103,125\).
\(1728,125\).
\(250\).
\(750\).
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
|
Điện lượng (nghìn mAh) |
[0,9;0,95) |
[0,95;1,0) |
[1,0;1,05) |
[1,05;1,1) |
[1,1;1,15) |
|
Số viên pin |
10 |
20 |
35 |
15 |
5 |
Tìm khoảng tứ phân vị của dãy số liệu trên (làm tròn kết quả cuối cùng đến hàng phần trăm, không làm tròn các kết quả trung gian).
\(0,68\).
\(0,07\).
\(0,86\).
\(0,7\).
