20 câu Trắc nghiệm Toán 11 Kết nối tri thức Bài 31. Định nghĩa và ý nghĩa của đạo hàm có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hàm số \(y = f(x)\) có đạo hàm tại \({x_0}\) là \(f'({x_0})\). Khẳng định nào sau đây là sai?
\(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x + {x_0}) - f({x_0})}}{{x - {x_0}}}\).
\(f'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}}\).
\(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\).
\(f'({x_0}) = \mathop {\lim }\limits_{h \to 0} \frac{{f(h + {x_0}) - f({x_0})}}{h}\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) thỏa mãn \(\mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right) - f\left( 3 \right)}}{{x - 3}} = 2\). Kết quả đúng là
\(f'\left( 2 \right) = 3\).
\(f'\left( x \right) = 2\).
\(f'\left( x \right) = 3\).
\(f'\left( 3 \right) = 2\).
Hệ số góc của tiếp tuyến với đồ thị hàm số y = f(x) = x2 tại điểm có hoành độ x0 = −2 là
−4.
4.
2.
−2.
Trong các khẳng định dưới đây. Tìm khẳng định đúng.
\(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\).
(C)' = C, C là hằng số.
Hệ số góc của tiếp tuyến tạo điểm M(x0; f(x0)): f(x).
Phương trình tiếp tuyến của đồ thị hàm số tại M(x0; f(x0)): y = f'(x)(x – x0) + f(x0).
Cho hàm số f(x) = 2x2 có đồ thị (C). Tiếp tuyến của đồ thị (C) tại điểm x0 = 1 có hệ số góc bằng
2.
−4.
1.
4.
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} - 3x\) tại điểm có hoành độ bằng 2.
\[y = - 9x + 16\].
\[y = - 9x + 20\].
\[y = 9x - 20\].
\[y = 9x - 16\].
Phương trình tiếp tuyến của đồ thị hàm số y = x3 tại điểm có tung độ bằng 8 là
y = −12x + 16.
y = 8.
y = 12x – 16.
y = 12x – 24.
Hệ số góc k của tiếp tuyến của đồ thị hàm số y = x2 – 4 tại điểm x0 là
\(k = x_0^2\).
k = 2x0.
k = −2x0.
k = −1.
Một chất điểm chuyển động có phương trình \[s = 2{t^2} + 3t\](\[t\]tính bằng giây, \[s\]tính bằng mét). Vận tốc của chất điểm tại thời điểm \[{t_0} = 2\](giây) bằng
\(22\left( {m/s} \right)\).
\(19\left( {m/s} \right)\).
\(9\left( {m/s} \right)\).
\(11\left( {m/s} \right)\).
Một chất điểm chuyển động có phương trình \(s = 2{t^2}\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc của chất điểm tại thời điểm \({t_0} = 2\) (giây) bằng.
\(8{\rm{ }}\left( {m/s} \right)\).
\(4{\rm{ }}\left( {m/s} \right)\).
\({\rm{9 }}\left( {m/s} \right)\).
\(11{\rm{ }}\left( {m/s} \right)\).
a) \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}}\).
b) \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 2x - 3}}{{x - 1}}\).
c) \(f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \left( {x + 4} \right)\).
d) \(f'\left( 1 \right) = a \Rightarrow a > 5\).
a)\(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f(\left( x \right) - f\left( 0 \right)}}{{x - 0}}\).
b) \(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{4}{{x + 1}}\).
c) Phương trình \({3^x} = 3\) có nghiệm bằng \(x = a - 2\).
d) \({\log _a}9 = 3\).
a) Có \(\mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right) - f\left( 3 \right)}}{{x - 3}} = 9\).
b) Tiếp tuyến của (C) tại điểm có hoành độ bằng 3 song song với đường thẳng 3x – y + 7 = 0.
c) Tiếp tuyến của (C) tại điểmM(3; f(3)) có phương trình là y = 6x – 10.
d) Tiếp tuyến của (C) tại điểm M(3; f(3)) cách điểm I(6; −11) một khoảng bằng 6.
a) Hệ số góc của tiếp tuyến của \((C)\) tại điểm \(M\) bằng \(6\).
b) Phương trình tiếp tuyến của \((C)\) tại \(M\) đi qua điểm \(A\left( {0;4} \right)\).
c) Phương trình tiếp tuyến của \((C)\) tại \(M\) cắt đường thẳng \(d:y = 3x\) tại điểm có hoành độ bằng 4.
d) Phương trình tiếp tuyến của \((C)\) tại \(M\) vuông góc với đường thẳng \(\Delta :y = - \frac{1}{6}x\).
a) Vận tốc của chất điểm tại thời điểm \(t = \frac{1}{2}\) giây là \(S'\left( {\frac{1}{2}} \right) = \mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{\frac{1}{2}g{t^2} - \frac{1}{8}g}}{{t - \frac{1}{2}}}\).
b) Nếu \(\mathop {\lim }\limits_{x \to 2} \frac{{\frac{1}{2}g{t^2} - 2g}}{{t - 2}} = 2g\)thì chất điểm đạt vận tốc là 2.
c) Vận tốc của chất điểm được xác định bởi công thức V(t) = S'(t) = gt.
d) Khi chạm đất thì chất điểm đạt vận tốc V(t) = 40 m/s.
PHẦN II. TRẢ LỜI NGẮN
Một chất điểm chuyển động thẳng xác định bởi phương trình \(s(t) = \frac{1}{2}{t^2}\), trong đó \(t\) là thời gian tính bằng giây và \(s\) là quãng đường đi được trong \(t\) giây tính bằng mét. Tính vận tốc (m/s) tức thời của chất điểm tại \(t = 5\).
Tính đạo hàm của hàm số \(f(x) = 2{x^3} + 1\) tại \({x_0} = 2\).
Cho hàm số \(y = f(x) = - 2{x^3} + x\) có đồ thị \((C)\).
Tính hệ số góc của tiếp tuyến của đồ thị \((C)\) tại điểm có hoành độ bằng 1 ;
Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số \(Q(t) = 2{t^2} + t\), trong đó \(t\) được tính bằng giây và \(Q\) được tính theo Culông. Tính cường độ dòng điện tại thời điểm \(t = 4(\;s)\).
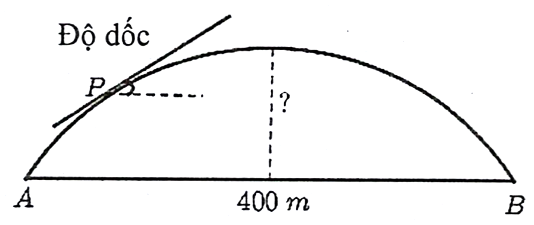
Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là \(400\;m\). Độ dốc của mặt cầu không vượt quá \(10^\circ \) (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chữ số thập phân thứ nhất).