20 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 26. Khoảng cách có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình chóp S.ABCD đáy là hình vuông ABCD cạnh a, cạnh bên SA vuông góc với mặt phẳng (ABCD) và SD = 2a. Tính khoảng cách từ S đến mặt phẳng (ABCD).
\(a\sqrt 5 \).
\(\frac{a}{2}\).
3a.
\(a\sqrt 3 \).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ^ (ABC). Gọi H và K lần lượt là hình chiếu của A lên SB và SC. Mệnh đề nào sau đây sai?
d(S, (ABC)) = SA.
d(C, (SAB)) = BC.
d(A, (SBC)) = AH.
d(A, (SBC)) = AK.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA ^ (ABCD). Gọi I là trung điểm của SC. Khoảng cách từ I đến mặt phẳng (ABCD) bằng độ dài đoạn thẳng nào?
IB.
IC.
IA.
IO.
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a (tham khảo hình vẽ).
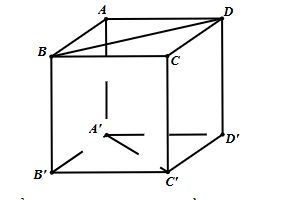
Khoảng cách giữa hai đường thẳng BD và A'C' bằng
a.
\(\sqrt 2 a\).
\(\frac{{\sqrt 3 }}{2}a\).
\(a\sqrt 3 \).
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {BCD} \right)\) bằng:
\(\frac{{a\sqrt 3 }}{4}\).
\(\frac{{a\sqrt 3 }}{3}\).
\(\frac{{a\sqrt 6 }}{3}\).
\(\frac{{a\sqrt 6 }}{2}\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\). Tính khoảng cách \(d\) giữa hai đường thẳng \(SB\) và \(CD\).
\(d = 2a\).
\(d = a\sqrt 3 \).
\(d = a\sqrt 2 \).
\(d = a\).
Cho lăng trụ tam giác đều \[ABC.A'B'C'\] có \[AB = a\], \[AA' = 2a\]. Khoảng cách giữa \(AB'\) và \[CC'\] bằng
\(\frac{{2a\sqrt 5 }}{5}\).
\(a\).
\(a\sqrt 3 \).
\(\frac{{a\sqrt 3 }}{2}\).
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính khoảng cách giữa hai đường thẳng BB', AD. 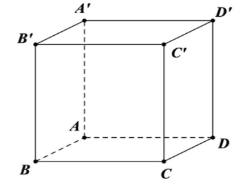
\(\frac{{a\sqrt 2 }}{2}\).
\(a\sqrt 2 \).
a.
\(\frac{{a\sqrt 3 }}{3}\).
Hình chóp S.ABC có SA ^ (ABC), tam giác ABC vuông tại A với AB = a; \(AC = a\sqrt 3 \). Khoảng cách giữa hai đường thẳng SA, BC bằng
\(\frac{{a\sqrt 2 }}{3}\).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
\(\frac{{a\sqrt 3 }}{3}\).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng
a.
\(\frac{{a\sqrt 5 }}{2}\).
\(\frac{{a\sqrt 3 }}{2}\).
\(a\sqrt 2 \).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi H là hình chiếu vuông góc của B lên B'D. Khi đó:
a) Khoảng cách từ điểm B đến đường thẳng DB' là BH.
b) Độ dài đoạn \(BH = \frac{{a\sqrt 6 }}{4}\).
c) d(B, AC) \( = \frac{1}{2}AC\).
d) d(B, AA') = BA'.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\) (tham khảo hình vẽ).
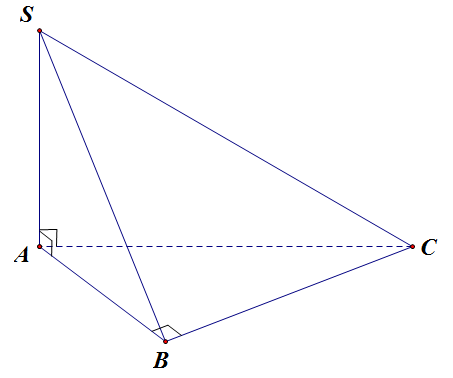
a) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) là đoạn \(BC\).
b) \[BC \bot \left( {SAB} \right)\].
c) Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) là đoạn \(AB\).
d) \[SB \bot BC\].
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và đáy \(ABCD\) là hình vuông tâm \(O\).
a) \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \widehat {SBA}\).
b) \(d\left( {D,\left( {SAC} \right)} \right) = DO\).
c) \[\left( {SC,\left( {SAD} \right)} \right) = \widehat {CSD}\].
d) \[d\left( {CD,SB} \right) = BD\].
Cho hình chóp \(S.ABCD\) có \(SA \bot (ABCD),SA = a\sqrt 3 ,ABCD\) là hình vuông cạnh bằng \(a\). Khi đó:
a) \[d(A,(SBC)) = \frac{{\sqrt 3 }}{3}a\].
b) \(AD//(SBC)\).
c) \(d(D,(SBC)) = \frac{{\sqrt 3 }}{2}a\).
d) Gọi \(M\) là trung điểm \(SA\). Khi đó: \(d(M,(SBC)) = \frac{{\sqrt 3 }}{4}a\).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA ^ (ABCD). Biết góc phẳng nhị diện [S, BC, A] = 60°.
a) BD ^ SC.
b) [S, BC, A] = \(\widehat {SBA}\).
c) d(S, (ABCD)) = \(a\sqrt 2 \).
d) \(d\left( {C,(SBD)} \right) = \frac{{a\sqrt 2 }}{2}\).
PHẦN II. TRẢ LỜI NGẮN
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2, cạnh bên SA vuông góc với đáy và SA = \(\sqrt 3 \). Khoảng cách từ D đến mặt phẳng (SBC) bằng bao nhiêu? (kết quả làm tròn đến hàng phần trăm).
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AC = 6, AB = 12. Biết SA vuông góc với mặt phẳng đáy và SA = 3. Gọi M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng SM và BC.
Cho hình lập phương ABCD.A'B'C'D' cạnh 2. Tính khoảng cách giữa hai mặt phẳng (A'BD), (CB'D'). (kết quả làm tròn đến hàng phần trăm).
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có BC = 2, \(AB = \sqrt 3 \). Tính khoảng cách từ AA' đến mặt phẳng (BCC'B') (kết quả làm tròn đến hàng phần trăm).
Cho hình chóp đều \(S.ABC\) có độ dài cạnh đáy bằng 1 và độ dài cạnh bên là 2. Tính khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) (làm tròn kết quả đến hàng phần trăm).



