20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài tập cuối chương IV (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi
Hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
Hai đường thẳng không có điểm chung.
Hai đường thẳng cùng nằm trong một mặt phẳng.
Hai đường thẳng cùng song song với đường thẳng thứ ba.
Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi
Đường thẳng đó song song với một đường thẳng thuộc mặt phẳng.
Đường thẳng và mặt phẳng không có điểm chung.
Đường thẳng đó không có điểm chung với một đường thẳng thuộc mặt phẳng.
Đường thẳng đó không có điểm chung với hai đường thẳng thuộc mặt phẳng.
Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi
Có một mặt phẳng chứa hai đường thẳng phân biệt cùng song song với mặt phẳng còn lại.
Hai mặt phẳng cùng song song với một đường thẳng.
Hai mặt phẳng cùng song song với mặt phẳng thứ ba.
Hai mặt phẳng không có điểm chung.
Phát biểu nào sau đây là sai?
Hình biểu diễn của một đường tròn có thể là một elip.
Hình biểu diễn của một hình thang (không phải là hình bình hành) có thể là một hình bình hành.
Hình biểu diễn của một tam giác đều có thể là một tam giác.
Hình biểu diễn của một hình vuông có thể là một hình bình hành.
Cho hình chóp S.ABCD, đáy là hình thang, đáy lớn AB, giao tuến của mặt (SAD) và (SBC) là
Sx với Sx // AB.
SK với K = AC Ç BD.
SK với K = AD Ç BC.
SK với K = AB Ç CD.
Cho tứ diện ABCD, gọi M, N, K lần lượt là trung điểm của AB, BC, CD. Trong các khẳng định sau, khẳng định nào đúng?
AD song song với mặt phẳng (MNK).
Hai đường thẳng MK và AC cắt nhau.
Giao tuyến của hai mặt phẳng (MNK) và mặt phẳng (ABD) đi qua trung điểm của AD.
Hai đường thẳng MN và BD cắt nhau.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm của DSAB, DSAD và E, F là trung điểm của AB, AD. Mệnh đề nào dưới đây đúng?
IJ // (SBD).
IJ // (SAD).
IJ // (SAB).
IJ // (SFE).
Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng (AB'D') song song với mặt phẳng
(ABCD).
(BCC'B').
(BDC').
(BDA').
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD. Gọi M là trung điểm của cạnh SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây là mệnh đề đúng?
MN // CD.
MN và SC cắt nhau.
MN và CD chéo nhau.
MN và SD cắt nhau.
Cho hình hộp ABCD. A'B'C'D'. Gọi M, M' lần lượt là trung điểm của các cạnh BC, B'C'. Hình chiếu của DB'DM qua phép chiếu song song trên (A'B'C'D') theo phương AA' là.
DB'D'M'.
DC'D'M'.
DDMM'.
DB'A'M'.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành (tham khảo hình bên). Gọi M là trung điểm của cạnh BC, I là điểm thuộc cạnh SC sao cho SI = 2IC. Gọi P là giao điểm của AC và (SMD). Gọi K là giao điểm của AI và (SMD).
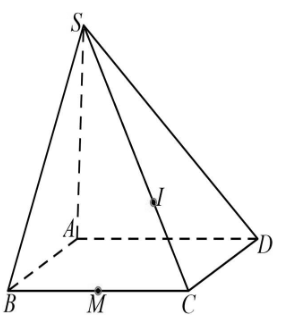
a) Ta có P cũng là giao điểm của hai đường thẳng AC và SD.
b) Ta có K cũng là giao điểm của hai đường thẳng AI và SP.
c) Đường thẳng IP song song với mặt phẳng (SAB).
d) Đường thẳng SD cắt mặt phẳng (IMA) tại H. Gọi \(\frac{{MK}}{{MH}} = \frac{a}{b}\) trong đó a, b là hai số nguyên dương và \(\frac{a}{b}\) là phân số tối giản. Khi đó a + b = 7.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm M, N lần lượt là trung điểm của các đoạn thẳng SB, SD.
a) Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với AD.
b) Đường thẳng MN song song với mặt phẳng (SBD).
c) Mặt phẳng (SAC) đi qua trung điểm của đoạn thẳng MN.
d) Nếu gọi I là giao điểm của mặt phẳng (AMN) với đường thẳng SC thì \(SI = \frac{1}{2}IC\).
Trong không gian cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Gọi G1; G2 lần lượt là trọng tâm của các tam giác SAD, SCD. Khi đó:
a) Đường thẳng G1G2 và AC có một điểm chung.
b) Giao tuyến của hai mặt phẳng (SAB) và (ABCD) là đường thẳng AB.
c) Đường thẳng G1G2 song song với mặt phẳng (ABCD).
d) Mặt phẳng chứa đường thẳng G1G2 và song song với mặt phẳng (ABCD) cắt các cạnh SA, SB, SC, SD lần lượt là M, N, E, F. Khi đó, tứ giác MNEF là hình bình hành.
Cho hình lăng trụ tam giác ABC. A'B'C'. Gọi M, N lần lượt là trung điểm A'B', AB và I là tâm của hình bình hành BCC'B'.
a) Điển N là hình chiếu song song của điểm M lên mặt phẳng (ABC) theo phương CC'.
b) Hình chiếu song song của tam giác A'CI lên mặt phẳng (ABC) theo phương CC' là tam giác ACN.
c) Giao tuyến của mặt phẳng (MIN) và mặt phẳng (BCC'B') là đường thẳng qua I và song song với BB'.
d) Đường thẳng MI cắt mặt phẳng (ABC) tại điểm K. Khi đó NK = AC.
Cho hình bình hành ABCD và một điểm S không thuộc mặt phẳng (ABCD), các điểm M, N lần lượt là trung điểm của đoạn thẳng AB, SC. Gọi O = AC Ç BD.
a) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Giao điểm I của đường thẳng AN và mặt phẳng (SBD) là điểm nằm trên đường thẳng SD.
c) Giao điểm J của đường thẳng MN và mặt phẳng (SBD) là điểm nằm trên đường thẳng SO.
d) Ba điểm I, J, B thẳng hàng.
PHẦN II. TRẢ LỜI NGẮN
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA, BC và P là điểm nằm trên cạnh AB sao cho \(AP = \frac{1}{3}AB.\) Gọi Q là giao điểm của SC và (MNP). Tính tỉ số \(\frac{{SQ}}{{SC}}\) (làm tròn kết quả đến hàng phần mười).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của AB, AD và SO. Gọi K là giao điểm của SC với mặt phẳng (MNP). Tính tỉ số \(\frac{{SK}}{{SC}}\).
Cho hình chóp S.ABCD có đáy là hình bình hành, trên cạnh SA lấy điểm M sao cho MA = 2MS. Gọi O là tâm của hình bình hành ABCD. Một phép chiếu song song theo phương MO lên mặt phẳng (ABCD) biến điểm S thành điểm N. Tính \(\frac{{CN}}{{CA}}\).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của BC, CD, SD. Gọi Q là giao điểm của SA với (MNP). Tính tỉ số \(\frac{{SQ}}{{SA}}\).
Cho hình chóp S.ABCD có đáy là hình bình hành. Trên cạnh SC lấy điểm M sao cho \(SM = \frac{1}{2}SC\). Mặt phẳng (P) chứa AM và song song với BD. Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB, SD. Tính tỉ số \(\frac{{SE}}{{SB}} + \frac{{SF}}{{SD}}\) (kết quả làm tròn đến hàng phần mười).
