20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho hình chóp đều S.ABCD, gọi O là tâm của đa giác đáy (tham khảo hình vẽ).
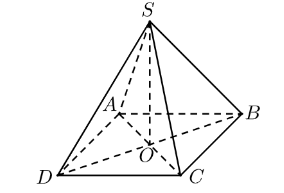
Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng góc nào sau đây?
\(\widehat {SBA}\).
\(\widehat {SBO}\).
\(\widehat {SOB}\).
\(\widehat {SBC}\).
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ). Giá trị sin của góc giữa đường thẳng AC' và mặt phẳng (ABCD) bằng 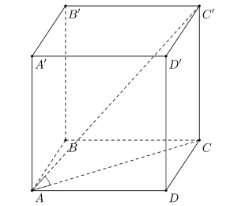
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{{\sqrt 2 }}{2}\).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.Gọi M là trung điểm của SD. Tan của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
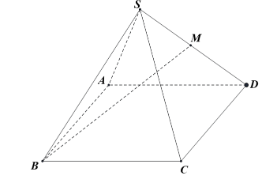
\(\frac{{\sqrt 2 }}{2}\).
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{2}{3}\).
\(\frac{1}{3}\).
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), \(SA = a\sqrt 2 \), tam giác ABC vuông cân tại B và \(AB = a\sqrt 2 \)(tham khảo hình vẽ). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 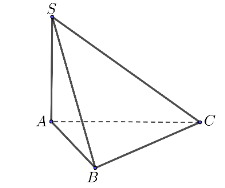
30°.
45°.
60°.
90°.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, cạnh bên SA ^ (ABCD) và \(SA = a\sqrt 2 \). Góc giữa đường thẳng SC và mặt phẳng (SAD) bằng
30°.
45°.
60°.
90°.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SA ^ (ABCD). Gọi H là hình chiếu của A lên BD và K là hình chiếu của A lên SD. Góc phẳng nhị diện [S, BD, A] là
\(\widehat {SKA}\).
\(\widehat {SBA}\).
\(\widehat {SHA}\).
\(\widehat {SDA}\).
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = BC = a, \(SA = a\sqrt 3 \), SA ^ (ABC). Góc nhị diện [S, BC, A] có số đo bằng
45°.
60°.
90°.
30°.
Cho hai mặt phẳng (P), (Q) có giao tuyến là đường thẳng CD. Điểm A Î (P); B Î (Q) và AO, BO cùng vuông góc với CD. M là một điểm bất kì thuộc CD (M ≠ O). Xác định góc nhị diện [A, CD, B].![Xác định góc nhị diện [A, CD, B]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/8-1751859922.png)
\(\widehat {AOB}\).
\(\widehat {AMO}\).
\(\widehat {AMB}\).
\(\widehat {OAB}\).
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và \(OB = OC = a\sqrt 6 \), OA = a. Tính góc nhị diện [A, BC, O].
45°.
60°.
90°.
30°.
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh 2a, \(SA = a\sqrt 6 \) và vuông góc với đáy. Số đo của góc nhị diện [S, BD, A].
45°.
60°.
90°.
30°.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = a. Gọi E, F lần lượt là hình chiếu của A lên SB, SD. Khi đó:
a) Góc giữa đường thẳng AE và mặt phẳng (SBC) bằng 90°.
b) Góc giữa đường thẳng AF và mặt phẳng (SCD) bằng 60°.
c) Góc giữa đường thẳng SA và mặt phẳng (SBC) bằng 45°.
d) Góc giữa đường thẳng SC và mặt phẳng (AEF) bằng 30°.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\)vuông góc với mặt phẳng đáy và \(SA = a\sqrt 2 \).
a) \(AB\) là hình chiếu của \(SB\) trên mặt phẳng \((ABCD)\).
b) \((SB,(ABCD)) \approx 54,74^\circ \).
c) \((SC,(ABCD)) = 45^\circ \).
d) \((SC,(SAB)) = 60^\circ \).
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng \(2a\) và cạnh bên bằng \(3a\). Khi đó:
a) Gọi \(M\) là trung điểm A'B', ta có \(C'M = a\sqrt 2 \).
b) Góc phẳng nhị diện [C, A'B', C'] bằng 60°.
c) Gọi \(K\) là trung điểm \(AB\),\(M\) là trung điểm A'B', khi đó: A'B' ^ MK.
d) Góc phẳng nhị diện [A, A'B', C] bằng 30°.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Gọi H là trung điểm cạnh AB. Khi đó:
a) Góc phẳng nhị diện [C, SH, B] là \(\widehat {CHB}\).
b) Góc phẳng nhị diện [C, SH, A] là \(\widehat {CHA}\).
c) Góc phẳng nhị diện [S, AB, C] là \(\widehat {SHC}\).
d) Số đo góc phẳng nhị diện [S, AB, C] bằng 30°.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SA vuông góc với mặt phẳng (ABCD), SA = a, AB = a, AD = 2a. Khi đó:
a) \(\widehat {SOA}\) là góc phẳng nhị diện của góc [S, BD, A].
b) Số đo của góc nhị diện [A, BC, S] bằng 45°.
c) \(\widehat {SCA}\) là góc phẳng nhị diện của góc [S, CD, A].
d) Số đo của góc nhị diện [S, AB, D] bằng 90°.
PHẦN II. TRẢ LỜI NGẮN
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B có \(AC = a\sqrt 3 \), cạnh bên AA' = 3a. Góc giữa đường thẳng A'C và mặt phẳng (ABC) bằng bao nhiêu độ?
Một hộp phấn không bụi có dạng hình hộp chữ nhật, chiều cao hộp phấn bằng \(8,2\;cm\) và đáy của nó có hai kích thước là \(8,5\;cm;10,5\;cm\) (xem hình vẽ sau). Tìm góc phẳng nhị diện [A, B'D', A'] (tính theo độ, làm tròn kết quả đến hàng phần mười).
![Tìm góc phẳng nhị diện [A, B'D', A'] (tính theo độ, làm tròn kết quả đến hàng phần mười). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/18-1751860356.png)
Cho hình chóp S.ABCD có đáy là hình thoi tâm I, cạnh a và có \(\widehat {BAD} = 60^\circ \). Các cạnh bên \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi φ là góc nhị diện [S, BD, A]. Giá trị tanφ bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a. Gọi M, N lần lượt là trung điểm AC và B'C', α là góc giữa đường thẳng MN và mặt phẳng (A'B'C'D'). Tính giá trị của sinα (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 ,SA \bot \left( {ABCD} \right)\). Góc giữa đường thẳng SD và mặt phẳng (ABCD) là α°. Tìm α.
