10 câu hỏi
Cho hình chóp đều S.ABCD, gọi O là tâm của đa giác đáy (tham khảo hình vẽ).
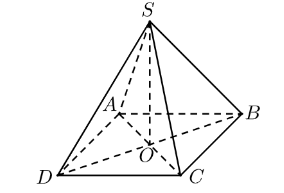
Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng góc nào sau đây?
\(\widehat {SBA}\).
\(\widehat {SBO}\).
\(\widehat {SOB}\).
\(\widehat {SBC}\).
Cho hình lập phương ABCD.A'B'C'D' (tham khảo hình vẽ). Giá trị sin của góc giữa đường thẳng AC' và mặt phẳng (ABCD) bằng
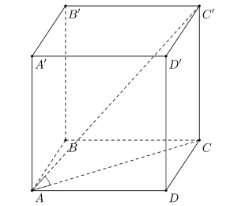
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{{\sqrt 6 }}{3}\).
\(\frac{{\sqrt 3 }}{2}\).
\(\frac{{\sqrt 2 }}{2}\).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a.Gọi M là trung điểm của SD. Tan của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
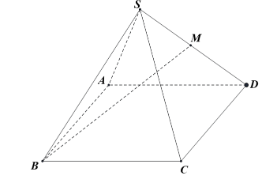
\(\frac{{\sqrt 2 }}{2}\).
\(\frac{{\sqrt 3 }}{3}\).
\(\frac{2}{3}\).
\(\frac{1}{3}\).
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), \(SA = a\sqrt 2 \), tam giác ABC vuông cân tại B và \(AB = a\sqrt 2 \)(tham khảo hình vẽ). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng
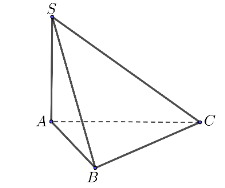
30°.
45°.
60°.
90°.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, cạnh bên SA ^ (ABCD) và \(SA = a\sqrt 2 \). Góc giữa đường thẳng SC và mặt phẳng (SAD) bằng
30°.
45°.
60°.
90°.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SA ^ (ABCD). Gọi H là hình chiếu của A lên BD và K là hình chiếu của A lên SD. Góc phẳng nhị diện [S, BD, A] là
\(\widehat {SKA}\).
\(\widehat {SBA}\).
\(\widehat {SHA}\).
\(\widehat {SDA}\).
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = BC = a, \(SA = a\sqrt 3 \), SA ^ (ABC). Góc nhị diện [S, BC, A] có số đo bằng
45°.
60°.
90°.
30°.
Cho hai mặt phẳng (P), (Q) có giao tuyến là đường thẳng CD. Điểm A Î (P); B Î (Q) và AO, BO cùng vuông góc với CD. M là một điểm bất kì thuộc CD (M ≠ O). Xác định góc nhị diện [A, CD, B].![Xác định góc nhị diện [A, CD, B]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/8-1751859922.png)
\(\widehat {AOB}\).
\(\widehat {AMO}\).
\(\widehat {AMB}\).
\(\widehat {OAB}\).
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và \(OB = OC = a\sqrt 6 \), OA = a. Tính góc nhị diện [A, BC, O].
45°.
60°.
90°.
30°.
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh 2a, \(SA = a\sqrt 6 \) và vuông góc với đáy. Số đo của góc nhị diện [S, BD, A].
45°.
60°.
90°.
30°.
