20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 4. Hàm số lượng giác và đồ thị (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Tập xác định của hàm số \(y = \tan x\) là:
\(\mathbb{R}{\rm{\backslash }}\left\{ 0 \right\}\).
\(\mathbb{R}{\rm{\backslash }}\left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\)
ℝ.
\(\mathbb{R}{\rm{\backslash }}\left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).
Tập xác định của hàm số \(y = 2\sin x\)là
\(\left[ {0;2} \right]\).
\(\left[ { - 1;1} \right]\).
\(\mathbb{R}\).
\(\left[ { - 2;2} \right]\).
Tập xác định của hàm số \(y = \cot x\) là:
\[\mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\].
\[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\].
Tập xác định của hàm số \(y = \tan 2x\) là
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\).
\(D = \mathbb{R}\backslash \left\{ {k\frac{\pi }{2},k \in \mathbb{Z}} \right\}\).
Cho các hàm số: \(y = \sin 2x\), \(y = \cos x\), \(y = \tan x\), \(y = \cot x\). Có bao nhiêu hàm số tuần hoàn với chu kỳ \(T = \pi \).
1
2
3
4
Khẳng định nào dưới đây là sai?
Hàm số\(y = \sin x\) là hàm số lẻ.
Hàm số\(y = \cos x\)là hàm số lẻ.
Hàm số\(y = \tan x\) là hàm số lẻ.
Hàm số\(y = \cot x\) là hàm số lẻ.
Hàm số nào sau đây là hàm số chẵn?
\(y = \cot 4x\).
\(y = \tan 6x\).
\(y = \sin 2x\).
\(y = \cos x\).
Khẳng định nào sau đây sai?
\(y = \tan x\) nghịch biến trong \(\left( {0;\;\frac{\pi }{2}} \right)\).
\(y = \cos x\) đồng biến trong \(\left( { - \frac{\pi }{2};\;0} \right)\).
\(y = \sin x\) đồng biến trong \(\left( { - \frac{\pi }{2};\;0} \right)\).
\(y = \cot x\) nghịch biến trong \(\left( {0;\;\frac{\pi }{2}} \right)\).
Hàm số nào sau đây nghịch biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?
\(y = \sin x\).
\(y = \cos x\).
\(y = \tan x\).
\(y = - \cot x\).
Tập giá trị của hàm số \(y = \sin 2x\) là:
\(\left[ { - 2;2} \right]\).
\(\left[ {0;2} \right]\).
\(\left[ { - 1;1} \right]\).
\(\left[ {0;1} \right]\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(y = 3 - \sin \left( {2x + \frac{\pi }{4}} \right)\). Khi đó:
a) Hàm số có tập xác định D = ℝ.
b) Giá trị nhỏ nhất của hàm số bằng 2.
c) Giá trị lớn nhất của hàm số bằng 4.
d) Tập giá trị của hàm số là T = [2; 4].
Cho hàm số f(x) = tan2x – 1. Khi đó:
a) Giá trị của hàm số f(x) tại \(x = \frac{\pi }{8}\) bằng 0.
b) Hàm số f(x) là hàm số chẵn.
c) Tập xác định của hàm số f(x) là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\) và tập giá trị là ℝ.
d) Hàm số f(x) là hàm số tuần hoàn.
Cho hàm số f(x) = 4sinx – 2. Khi đó:
a) Tổng giá trị lớn nhất và nhỏ nhất của hàm số f(x) = 4sinx – 2 bằng −4.
b) Hàm số f(x) = 4sinx – 2 là hàm số chẵn.
c) Hàm số f(x) = 4sinx – 2 có tập xác định là ℝ.
d) f(150°) = 0.
Cho hàm số \(y = \sin \left( {2x - \frac{\pi }{2}} \right)\).
a) Tập xác định của hàm số đã cho là [−1; 1].
b) Hàm số đã cho là hàm số lẻ.
c) Hàm số đã cho là hàm số tuần hoàn với chu kì T = π.
d) Giá trị lớn nhất của hàm số đã cho trên \(\left[ { - \frac{\pi }{8};\frac{\pi }{3}} \right]\) bằng 1.
Cho hàm số y = f(x) có đồ thị như sau
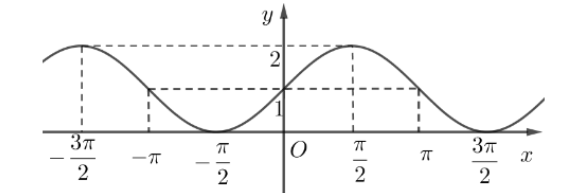
a) Hàm số có tập xác định \(D = \left[ { - \frac{{3\pi }}{2};\frac{{3\pi }}{2}} \right]\).
b) Hàm số đồng biến trên khoảng (−π; 0).
c) Hàm số nghịch biến trên khoảng \(\left( { - \pi ; - \frac{\pi }{2}} \right)\).
d) Tập giá trị của hàm số là [0; 2].
PHẦN II. TRẢ LỜI NGẮN
Tập giá trị của hàm số y = 5 + 4sin2xcos2x là T = [a; b]. Tính b – a.
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 31 + 3\sin \frac{\pi }{{12}}\left( {t - 9} \right)\), với h tính bằng độ C và t là thời gian trong ngày tính bằng giờ (0 < t ≤ 24). Tính nhiệt độ ngoài trời của thành phố đó vào lúc 19 giờ.
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 12\). Mực nước của kênh thấp nhất là bao nhiêu mét?
Một chất điểm dao động điều hòa theo phương trình \(s = 3\sin \left( {\frac{\pi }{2}t} \right)\) với s tính bằng cm và t tính bằng giây. Dựa vào đồ thị của hàm số sin, ta xác định được thời điểm t Î (a; b) trong 4 giây đầu thì \(s < - \frac{3}{2}\). Tính a + b.
Một con lắc lò xo dao động điều hòa quanh vị trí cân bằng theo phương trình y = 25sin4πt ở đó y được tính bằng centimets còn thời gian t được tính bằng giây.
Tìm chu kì dao động của con lắc lò xo.
