10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Hàm số nào sau đây đồng biến trên ℝ.
\(y = {\left( {\sqrt 5 - 2} \right)^x}\).
\(y = {\left( {\frac{3}{\pi }} \right)^x}\).
y = 0,7x.
\(y = {\left( {\frac{e}{2}} \right)^x}\).
Tập xác định của hàm số y = ln(x – 2) là
[2; +∞).
(2; +∞).
ℝ.
ℝ\{2}.
Hàm số nào sau đây không là hàm số mũ?
\(y = {\left( {\frac{2}{3}} \right)^x}\).
\(y = {\left( {\frac{2}{3}} \right)^{ - x}}\).
y = x7.
\(y = {\left( {\frac{e}{2}} \right)^x}\).
Cho hàm số y = 5x có tập xác định là
ℝ.
(0; +∞).
(−∞; 0).
(1; +∞).
Hàm số y = logax có đồ thị đi qua điểm nào sau đây?
(1; 0).
(a; 1).
(a2; 2).
Tất cả các điểm trên.
Cho a > 0, b > 1, a ≠ 1; b ≠ 1. Đồ thị hàm số y = ax và y = logbx được cho như hình vẽ bên. Trong các mệnh đề dưới đây, mệnh đề nào đúng?
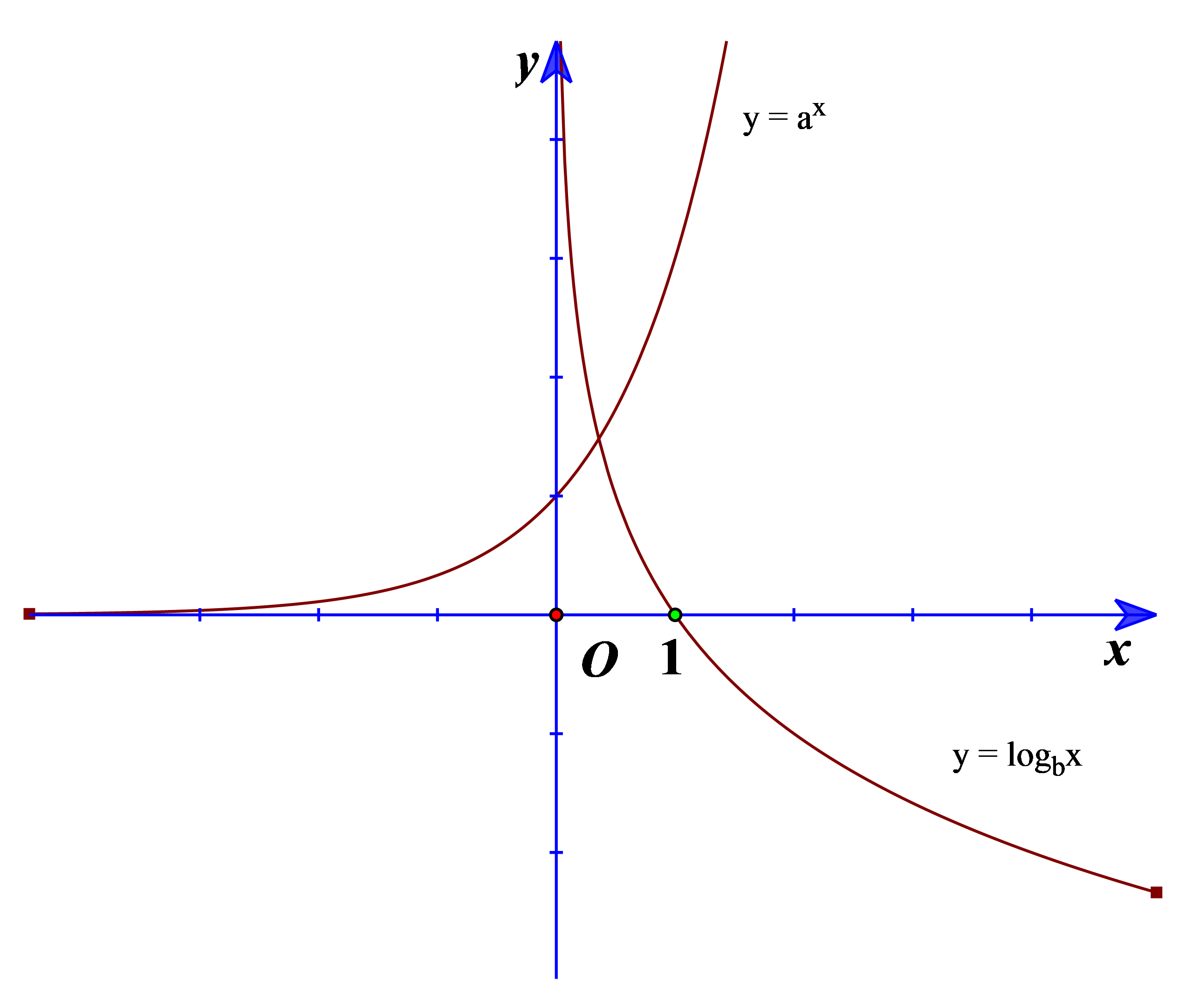
a > 1, b > 1.
a > 1, 0 < b < 1.
0 < a < 1, b > 1.
0 < a < 1, 0 < b < 1.
Tập xác định của hàm số y = log(x2 – 3x + 2) là
D = (−∞; 1) È (2; +∞).
D = (1; 2).
D = (−∞; 1] È [2; +∞).
D = [1; 2].
Cho đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?
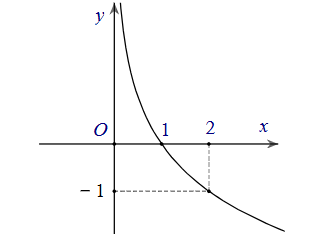
y = log4x.
y = log0,25x.
\(y = - \frac{1}{2}x\).
y = log0,5x.
Trong các bất đẳng thức sau, bất đẳng thức nào sai?
log35 > log3π.
log0,7e > log0,7π.
(0,3)e < (0,3)π.
log35 < log32.
Cho a > 1. Mệnh đề nào sau đây là đúng?
Tập xác định của hàm số y = logax là ℝ.
Tập giá trị của hàm số y = ax là ℝ.
Tập giá trị của hàm số y = logax là ℝ.
Tập xác định của hàm số y = ax là (0; +∞).
