20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 1. Hai đường thẳng vuông góc (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong các mệnh đề sau, mệnh đề nào đúng?
Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc (IE, JF) bằng
30°.
45°.
60°.
90°.
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng
90°.
45°.
30°.
60°.
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng nhau. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng
90°.
45°.
30°.
60°.
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Số đo góc giữa hai đường thẳng SA và CD bằng
90°.
45°.
30°.
60°.
Cho lăng trụ ABC.A'B'C' có tất cả các cạnh bằng nhau (tham khảo hình vẽ)Góc giữa hai đường thẳng AB và C'A' bằng 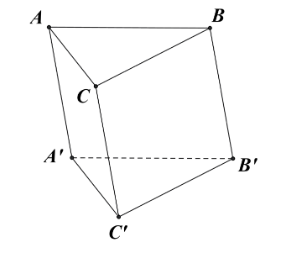
30°.
60°.
45°.
90°.
Trong không gian, cho hai đường thẳng a và b vuông góc với nhau. Khi đó:
Hai đường thẳng a và b có thể cắt nhau hoặc chéo nhau.
Hai đường thẳng a và b luôn cắt nhau.
Hai đường thẳng a và b chéo nhau.
Hai đường thẳng a và b song song với nhau.
Trong không gian cho hai đường thẳng a và b song song với nhau, nếu đường thẳng c vuông góc với đường thẳng a thì
Đường thẳng c vuông góc với đường thẳng b.
Đường thẳng c song song với đường thẳng b.
Đường thẳng c song song hoặc trùng với đường thẳng b.
Đường thẳng c cắt đường thẳng b tại một điểm.
Trong hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau. mệnh đề nào sai?
BB' ^ BD.
A'C' ^ BD.
A'B ^ DC'.
BC' ^ A'D.
Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA = SC, SB = SD. Trong các mệnh đề sau mệnh đề nào sai?
AC ^ SD.
BD ^ AC.
BD ^ SA.
AC ^ SA.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABCD có đáy là vuông cạnh a. Cạnh bên SA = a và vuông góc với AB và AD, \(SC = a\sqrt 3 \). Khi đó:
a) SA ^ BC.
b) SA ^ CD.
c) BC ^ SB.
d) K là hình chiếu của A lên SB thì SC ^ AK.
Cho tứ diện đều \(ABCD\) có cạnh bằng \(a,M\) là trung điểm cạnh \(BC\), \(N\) là trung điểm của \(AC\). Khi đó:
a) \(MN//AB\).
b) \(MD = ND = \frac{{a\sqrt 2 }}{2}\).
c) \((AB,DM) = (MN,DM)\).
d) \(\cos (AB,DM) = \frac{{\sqrt 3 }}{3}\).
Cho hình chóp \(S.ABCD\) có đáy là hình thoi. Gọi \(M,N\) theo thứ tự là trung điểm của đoạn \(SB,SD\). Khi đó:
a) \(MN//BD\).
b) \(MN\) và \(AC\) là hai đường thẳng chéo nhau.
c) \(AC \bot BD\).
d) \((MN,AC) = 90^\circ \).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Tam giác SAB vuông cân tại S và \(\widehat {BSC} = 60^\circ \); SA = a. Gọi M, N lần lượt là trung điểm cạnh SB, SA, φ là góc giữa đường thẳng AB và CM.
a) Độ dài đoạn thẳng AB bằng \(a\sqrt 3 \).
b) Tam giác SBC là tam giác đều.
c) MN // AB và (AB, CM) = (MN, CM).
d) Côsin góc tạo bởi hai đường thẳng AB và CM bằng \(\frac{{\sqrt 6 }}{8}\).
Cho hình lăng trụ tam giác ABC.A'B'C' có AA' ^ AB, AA' ^ AC và tất cả các cạnh đều bằng a. Gọi M là trung điểm AA'. Khi đó
a) \(\left( {A'B,C'C} \right) = \widehat {AA'B}\).
b) (A'B, C'C) = 45°.
c) (A'C, MB) = \(\widehat {BAC}\).
d) (A'C, MB) ≈ 42,6°.
PHẦN II. TRẢ LỜI NGẮN
Cho tứ diện đều ABCD. Gọi M là trung điểm của cạnh BC. Cosin của góc giữa hai đường thẳng AB và DM bằng \(\frac{{\sqrt a }}{6}\). Tìm a.
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = a. Gọi M là trung điểm của AB. Góc giữa hai đường thẳng SM và BC bằng a°. Tìm a.
Cho tứ diện ABCD có AC = 6, BD = 8 có AC ^ BD. Gọi M, N lần lượt là trung điểm của AD, BC. Tính độ dài đoạn thẳng MN.
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a, O là tâm hình vuông ABCD. Gọi M, N lần lượt là trung điểm AB và SB. Gọi α là góc giữa hai đường thẳng MN và MO. Tính cosα.
Cho tứ diện ABCD có AB = CD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài đoạn thẳng MN biết góc giữa hai đường thẳng AB và MN bằng 30° (làm tròn kết quả đến hàng phần trăm).
