20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 1. Góc lượng giác (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Với ba tia Ou, Ov, Ow bất kì. Công thức nào sau đây là đúng:
(Ou, Ov) + (Ow, Ov) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) + (Ov, Ow) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) − (Ov, Ow) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
(Ou, Ov) − (Ow, Ov) = (Ou, Ow) + \[k360^\circ (k \in \mathbb{Z})\].
Công thức nào sau đây là đúng về mối quan hệ giữa góc và rad ?
\[1^\circ = \frac{\pi }{{360}}\] rad.
\[1^\circ = \frac{\pi }{{180}}\] rad.
\[1\,\,rad\,{\rm{ = }} - {\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^o}\].
\[1\,\,rad\,{\rm{ = }}{\left( {\frac{{{\rm{90}}}}{{\rm{\pi }}}} \right)^o}\].
Cho một góc lượng giác (Ox, Ou) có số đo−30° và một góc lượng giác (Ox, Ov) có số đo 120°. Tính số đo góc lượng giác (Ou, Ov).
\[150^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[ - 150^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[90^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
\[ - 90^\circ + {\rm{ }}k360^\circ (k \in \mathbb{Z})\].
Cho \[\widehat {{\rm{uOv}}}{\rm{ = 36}}^\circ \].Giá trị \[\widehat {{\rm{uOv}}}\]khi đổi sang rad là:
\[\frac{\pi }{4}\].
\[\frac{\pi }{5}\].
\[\frac{{3\pi }}{4}\].
\[\frac{{2\pi }}{5}\].
Cho \[\widehat {{\rm{uOv}}}{\rm{ = }}\frac{{{\rm{5\pi }}}}{{\rm{6}}}\]. Giá trị \[\widehat {{\rm{uOv}}}\] khi đổi sang độ là:
30°.
120°.
150°.
60°.
Trên đường tròn lượng giác, cho góc lượng giác có số đo \[\frac{\pi }{3}\] rad thì mọi góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác trên đều có số đo dạng:
\(\frac{\pi }{3}\).
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k}}\frac{{\rm{\pi }}}{{\rm{2}}}{\rm{,(k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
Góc lượng giác (Ox, Ot) có một số đo là \[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + 2023\pi , (k}} \in \mathbb{Z}{\rm{)}}\], số đo tổng quát của góc lượng giác (Ox, Ot) là:
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{\rm{\pi }}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
\[\frac{{{\rm{4\pi }}}}{{\rm{3}}}{\rm{ + k2\pi , (k}} \in \mathbb{Z}{\rm{)}}\].
Trên hình vẽ hai điểm \[M,N\] biểu diễn các cung có số đo là: 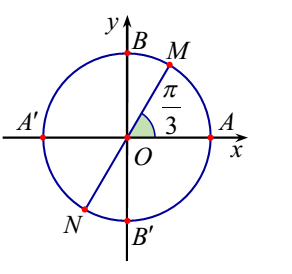
\[x = \frac{\pi }{3} + 2k\pi \].
\[x = - \frac{\pi }{3} + k\pi \].
\[x = \frac{\pi }{3} + k\pi \].
\[x = \frac{\pi }{3} + k\frac{\pi }{2}.\]
Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó M1M2M3M4 là hình vuông, \(\widehat {AO{M_1}} = 45^\circ \). Các điểm nào sau đây biểu diễn đẩy đủ các góc lượng giác \( - \frac{\pi }{2} + k2\pi \).
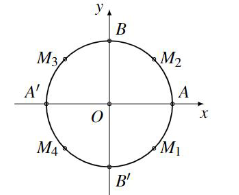
Điểm B'.
Điểm B, B'.
Điểm M4.
Điểm M4, M5.
Hình vẽ bên là vòng tròn lượng giác gốc A, trong đó M1M2M3M4 là hình vuông, \(\widehat {AO{M_1}} = 45^\circ \). Điểm A biểu diễn đầy đủ các góc lượng giác có số đo là: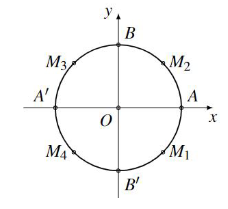
\[x = \frac{\pi }{4} + 2k\pi \].
\[x = \frac{{2\pi }}{3} + k\pi \].
\[k2\pi \].
\[k\pi .\]
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho một góc lượng giác (Ox, Ou) có số đo 250° và một góc lượng giác (Ox, Ov) có số đo −270°.
a) Số đo góc lượng giác (Ou, Ox) bằng −250° + k360°, k Î ℤ.
b) Số đo góc lượng giác (Ov, Ox) bằng 270° + k360°, k Î ℤ.
c) Số đo một góc lượng giác (Ou, Ov) bằng −20°.
d) Số đo một góc lượng giác (Ou, Ov) theo đơn vị radian bằng \(\frac{\pi }{9}\).
Cho hình vẽ sau:
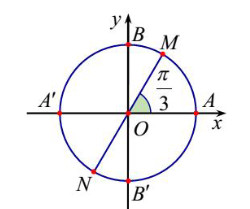
a) Số đo góc lượng giác (OM, OA) là (OM, OA) = \(\frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
b) (ON, OA) = (ON, OM) – (OA, OM).
c) Điểm B biểu diễn góc lượng giác có số đo \(\frac{\pi }{2}\).
d) Hai điểm M, N biểu diễn các cung có số đo là \(x = \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Cho góc lượng giác α có số đo theo đơn vị rađian là \(\frac{{3\pi }}{4}\).
a) Góc lượng giác α có số đo theo đơn vị độ là 155°.
b) Điểm biểu diễn góc lượng giác α là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I.
c) Góc lượng giác \( - \frac{{5\pi }}{4}\) có cùng điểm biểu diễn trên đường tròn lượng giác với góc α.
d) Góc lượng giác 855° có cùng điểm biểu diễn trên đường tròn lượng giác với góc α.
Cho các tia Ox, Oy, Oz, Ou, Ot như hình vẽ. Biết số đo các góc của góc hình học \(\widehat {xOy} = 60^\circ ;\widehat {xOz} = 150^\circ ;\widehat {xOt} = 30^\circ ;\widehat {xOu} = 110^\circ \).
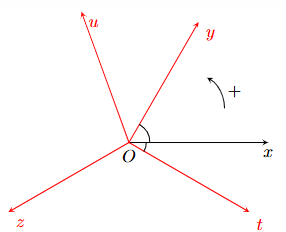
a) (Ox, Oy) = 60° + k360° (k Î ℤ).
b) (Ox, Oz) = 150° + k360° (k Î ℤ).
c) (Ox, Ot) = 30° + k360° (k Î ℤ).
d) (Ox, Ou) = 110° + k360° (k Î ℤ).
Cho đường tròn lượng giác có điểm gốc là điểm A (tham khảo hình bên).
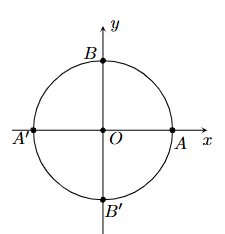
a) Điểm biểu diễn góc lượng giác có số đo \(\frac{\pi }{4}\) nằm trên cung AB.
b) Điểm biểu diễn góc lượng giác có số đo \( - \frac{\pi }{3}\) nằm trên cung BA'.
c) Điểm biểu diễn góc lượng giác có số đo \(\frac{{4\pi }}{5}\) nằm trên cùng A'B'.
d) Điểm biểu diễn góc lượng giác có số đo \(\frac{{ - 5\pi }}{9}\) nằm trên cung B'A.
PHẦN II. TRẢ LỜI NGẮN
Trên đường tròn lượng giác, có bao nhiêu điểm M thỏa mãn (OA, OM) = \(\frac{\pi }{3} + \frac{{k\pi }}{3},k \in \mathbb{Z}\).
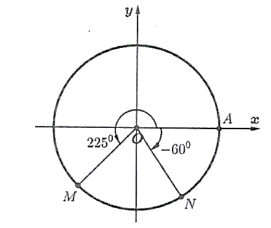
Từ hình vẽ đường tròn lượng giác, công thức số đo tổng quát của góc lượng giác (OA, OM); (OA, ON) có dạng lần lượt là n° + k360° (k Î ℤ); m° + k360° (k Î ℤ) với n, m là các số nguyên. Tính giá trị \(S = \frac{1}{4}{m^2} - n\).
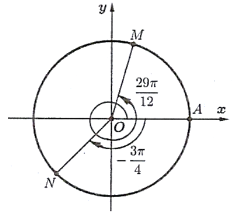
Từ hình vẽ đường tròn lượng giác, công thức số đo tổng quát của góc lượng giác (OA, OM); (OA, ON) có dạng lần lượt là \(\frac{n}{m}\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\); \( - \frac{p}{q}\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\) với m; n; p; q là các số nguyên và \(\frac{n}{m};\frac{p}{q}\) là phân số tối giản. Tính giá trị T = (m + p) – (n + q).
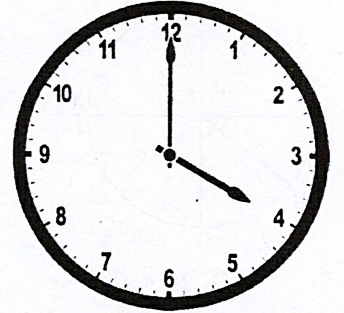
Một chiếc đồng hồ có kim giờ và kim phút được cho như trong hình vẽ sau. Xét tia \(Ou\) là kim giờ, \(Ov\) là kim phút. Xét chiều quay của góc là chiều kim đồng hồ, công thức số đo tổng quát của góc lượng giác \((Ou,Ov)\) = m° + k360°. Tìm m.
Một cái đồng hồ treo tường có đường kính bằng \(60\;cm\), ta xem vành ngoài chiếc đồng hồ là một đường tròn với các điểm \(A,B,C\) lần lượt tương ứng với vị trí các số \(2,9,4\). Tính tổng độ dài các cung nhỏ \(AB\) và \(AC\) (kết quả tính theo đơn vị centimét và làm tròn đến hàng đơn vị).


