10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong không gian, qua ba điểm không thẳng hàng xác định được bao nhiêu mặt phẳng?
1.
4.
3.
2.
Cho 4 điểm A, B, C, D không đồng phẳng (tham khảo hình vẽ bên). Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
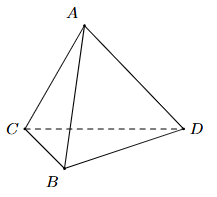
2.
4.
3.
6.
Cho bốn điểm A, B, C, D không cùng nằm trên một mặt phẳng. Trên AB, AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây?
(CMN).
(BCD).
(ABD).
(ACD).
Trong không gian, mệnh đề nào sau đây là mệnh đề sai?
Có duy nhất một đường thẳng đi qua hai điểm phân biệt.
Tồn tại duy nhất một mặt phẳng chứa hai đường thẳng cắt nhau.
Có duy nhất một mặt phẳng đi qua ba điểm phân biệt.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Chọn khẳng định sai trong các khẳng định sau.
Nếu ba điểm phân biệt M, N, P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
Cho tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (BCD) là
BC.
AB.
CD.
AD.
Cho hình chóp S.ABC. Gọi M là trung điểm của cạnh BC. Giao tuyến của hai mặt phẳng (SAM) và (SBC) là
SB.
SM.
SC.
BC.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là
SD.
SO (O là tâm của hình bình hành ABCD).
SE (E là trung điểm của AB).
SF (F là trung điểm của CD).
Cho hình chóp S.ABCD, có đáy ABCD là hình thang đáy lớn AB. Khi đó giao điểm của BC và (SAD) là
giao điểm của BC và SA.
giao điểm của BC và SD.
giao điểm của BC và AD.
giao điểm của AC và BD.
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. Khi đó giao điểm I của AM và (SBD) là
trọng tâm của tam giác SAC.
trung điểm của AM.
trung điểm của SO.
trọng tâm của tam giác SCD.
