20 câu trắc nghiệm Toán 11 Chân trời sáng tạo Bài 1. Biến cố giao và quy tắc nhân xác suất (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Một hộp có 30 tấm thẻ được đánh số từ 1 đến 30. Lấy ngẫu nhiên một tấm thẻ từ hộp. Xét các biến cố sau:
P: “Số ghi trên thẻ được lấy là số chia hết cho 2”.
Q: “Số ghi trên thẻ được lấy là số chia hết cho 4”.
Khi đó biến cố P Ç Q là
“Số ghi trên thẻ được lấy là số chia hết cho 8”.
“Số ghi trên thẻ được lấy là số chia hết cho 2”.
“Số ghi trên thẻ được lấy là số chia hết cho 6”.
“Số ghi trên thẻ được lấy là số chia hết cho 4”.
Cho A và B là hai biến cố độc lập. Mệnh đề nào dưới đây đúng?
Hai biến cố A và \(\overline B \) không độc lập.
Hai biến cố \(\overline A \) và \(\overline B \) không độc lập.
Hai biến cố \(\overline A \) và B độc lập.
Hai biến cố A và A È B độc lập.
Có hai hộp đựng bi. Hộp thứ nhất có 3 viên bi đỏ và 4 viên bi xanh. Hộp thứ hai có 5 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi. Xét các biến cố sau:
A: “Viên bi được lấy ở hộp thứ nhất có màu đỏ, ở hộp thứ hai có màu xanh”;
B: “Viên bi được lấy ở hộp thứ nhất có màu xanh, ở hộp thứ hai có màu đỏ”.
Khi đó hai biến cố A và B là
Hai biến cố độc lập với nhau.
Hai biến cố bằng nhau.
Hai biến cố đối của nhau.
Hai biến cố xung khắc.
Hai biến cố A và B được gọi là xung khắc khi và chỉ khi
A È B = W.
A È B = Æ.
A Ç B = W.
A Ç B = Æ.
Một cầu thủ sút bóng vào cầu môn hai lần, biết xác suất sút vào cầu môn là \(\frac{1}{3}\). Tính xác suất để cầu thủ sút bóng hai lần đều không vào cầu môn.
\(\frac{2}{9}\).
\(\frac{4}{3}\).
\(\frac{1}{9}\).
\(\frac{4}{9}\).
Cho A và B là hai biến cố độc lập với nhau, P(A) = 0,3; P(B) = 0,4. Khi đó P(AB) bằng
0,58.
0,7.
0,12.
0,1.
An và Bình không quen biết nhau và học ở hai nơi khác nhau. Xác suất để An và Bình đạt điểm giỏi về môn Toán trong kì thi cuối năm tương ứng là 0,92 và 0,88. Tính xác suất để cả An và Bình đều không đạt điểm giỏi.
0,8096.
0,0096.
0,3649.
0,3597.
Cho A, B là hai biến cố độc lập. Biết P(A) = 0,2 và P(B) = 0,5. Xác suất của biến cố \(\overline A B\) là
0,1.
0,4.
0,04.
0,01.
Một chiếc ô tô với hai động cơ độc lập đang gặp trục trặc kĩ thuật. Xác suất để động cơ 1 gặp trục trặc là 0,5. Xác suất để động cơ 2 gặp trục trặc là 0,4. Biết rằng xe chỉ không thể chạy được khi cả hai động cơ bị hỏng. Tính xác suất để xe đi được.
0,2.
0,9.
0,8.
0,1.
Có 2 bình, mỗi bình đựng 6 viên bi trắng và 5 viên bi đen. Lần lượt lấy ngẫu nhiên ra 1 viên bi từ bình thứ nhất và 1 viên bi từ bình thứ hai. Tính xác suất để lấy được viên bi thứ nhất màu trắng và viên bi thứ hai màu đen?
\(\frac{1}{{35}}\).
\(\frac{{35}}{{144}}\).
\(\frac{{30}}{{121}}\).
\(\frac{{23}}{{22}}\).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Có hai chuồng nuôi gà. Chuồng I có 5 con gà trống và 10 con gà mái. Chuồng II có 3 con gà mái và 7 con gà trống. Từ mỗi chuồng bắt ngẫu nhiên một con gà. Gọi:
A là biến cố: “bắt được gà mái từ chuồng I”;
B là biến cố: “bắt được gà trống từ chuồng II”. Khi đó:
a) n(A) = 10.
b) n(B) = 5.
c)\(P\left( A \right) = \frac{1}{3}\) và \(P\left( B \right) = \frac{7}{{10}}\).
d) Hai biến cố A và B độc lập.
Một hộp đựng 15 tấm thẻ cùng loại được đánh số từ 1 đến 15. Rút ngẫu nhiên một tấm thẻ, quan sát số ghi trên thẻ. Gọi A là biến cố “Số ghi trên tấm thẻ nhỏ hơn 9”, B là biến cố “Số ghi trên tấm thẻ là số nguyên tố nhỏ hơn 10” và C là biến cố “Số ghi trên tấm thẻ là số chẵn”. Khi đó:
a) AB là biến cố “Số ghi trên tấm thẻ là số nguyên tố nhỏ hơn 10”.
b) BC là biến cố “Số ghi trên tấm thẻ là số chẵn”.
c) Số kết quả thuận lợi cho biến cố AB là 4.
d) Không có kết quả thuận lợi cho biến cố BC.
Một xạ thủ bắn lần lượt hai viên đạn vào bia. Xác suất bắn không trúng đích của viên thứ nhất và viên thứ hai lần lượt là 0,2 và 0,3. Gọi biến cố A: “Lần thứ nhất bắn không trúng bia”, biến cố B: “Lần thứ hai bắn không trúng bia”. Khi đó:
a) A; B là hai biến cố độc lập.
b) Xác suất biến cố: “Cả hai lần bắn không trúng bia” là 0,06.
c) Xác suất biến cố: “Lần bắn thứ nhất trúng bia, lần bắn thứ hai không trúng bia” là 0,21.
d) Xác suất biến cố: “Có ít nhất một lần bắn trúng bia” là 0,94.
Trên một bảng quảng cáo, người ta mắc hai hệ thống bóng đèn. Hệ thống I gồm 2 bóng mắc nối tiếp, hệ thống II gồm 2 bóng mắc song song. Khả năng bị bỏng của mỗi bóng đèn sau 6 giờ thắp sáng liên tục là 0,15. Biết tình trạng của mỗi bóng đèn là độc lập. Khi đó xác suất để:
a) Hệ thống II bị hỏng (không sáng) bằng: 0,0225.
b) Từ đó suy ra xác suất để hệ thống II hoạt động bình thường bằng 0,9775.
c) Hệ thống I bị hỏng (không sáng) bằng: 0,5775.
d) Cả hai hệ thống bị hỏng (không sáng) (kết quả được làm tròn đến hàng phần trăm nghìn) khoảng 0,02624.
Một người vừa gieo một con xúc xắc để ghi lại số chấm xuất hiện, sau đó người này tiếp tục chọn ngẫu nhiên một lá bài từ bộ bài 52 lá. Tính xác suất để :
a) Gọi \(A\) là biến cố: "Số chấm của xúc xắc lớn nhất", khi đó: \(P(A) = \frac{1}{6}\).
b) Gọi \(B\) là biến cố: "Chọn được một lá bài tây", khi đó: \(P(B) = \frac{3}{{13}}\).
c) Xác suất để số chấm trên con xúc xắc là lớn nhất và chọn được một lá bài tây bằng \(\frac{1}{{26}}\).
d) Xác suất để số chấm trên con xúc xắc và số của lá bài là giống nhau bằng \(\frac{1}{{16}}\).
PHẦN II. TRẢ LỜI NGẮN
Gieo hai đồng xu A và B một cách độc lập. Đồng xu A được chế tạo cân đối. Đồng xu B được chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa. Tính xác suất để: Khi gieo hai đồng xu một lần thì cả hai đều ngửa. (làm tròn kết quả đến hàng phần mười).
Tại giải Đua xe công thức 1 (F1) được tổ chức tại Abu Dhabi, giải đấu quy tụ 11 tay đua đến từ các đội đua xe nổi tiếng trên thế giới. Trong đó có 2 ứng cử viên cho chức vô địch là L.Hamilton (Mercedes) và M.Verstappen (Red Bull) với tỉ lệ vô địch lần lượt là 0,72 và 0,79. Tom cùng bố đi xem và đặt cược buổi ăn sáng, anh đặt Verstappen sẽ vô địch. Tính xác suất để Tom thắng được buổi sáng (kết quả làm tròn đến hàng phần trăm).
Bài thực hành môn Công nghệ, bạn An gieo 1 hạt cà phê và 1 hạt sầu riêng vào 2 chậu khác nhau (mỗi chậu 1 hạt). Gọi A là biến cố “Hạt cà phê nảy mầm” và B là biến cố “Hạt sầu riêng nảy mầm”. Sơ đồ hình cây về xác suất của hai biến cố A và B như sau:
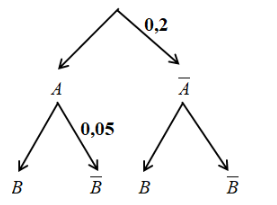
Xác suất để cả 2 hạt cà phê và sầu riêng đều nảy mầm là \(\frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản). Khi đó tích a.b bằng bao nhiêu?
Một bệnh truyền nhiễm có xác suất truyền bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Anh Quang tiếp xúc với 1 người bệnh hai lần, trong đó có một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất anh Quang không bị lây bệnh từ người bệnh mà anh tiếp xúc đó.
Jenny, Jim đang trò đang trò chuyện với Merry về việc có nên đi dự tiệc hay không. Xác suất Jenny sẽ tham dự là 0,4 và xác suất Jim sẽ tham dự là 0,6 , nhưng hôm đó Merry có việc bận nên khả năng không tham dự bữa tiệc là 0,8 . Tính xác suất để ba người bạn cùng tham dự (kết quả làm tròn đến hàng phần trăm).
