20 câu trắc nghiệm Toán 11 Cánh diều Bài 6. Hình lăng trụ đứng, hình chóp đều. Thể tích của một số hình khối (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hình lăng trụ đứng tam giác ABC.A'B'C'. Khẳng định nào sau đây sai?
Các mặt bên của lăng trụ là các hình chữ nhật bằng nhau.
Các cạnh bên của lăng trụ bằng nhau và vuông góc với đáy.
Hai mặt đáy song song với nhau.
Hai tam giác ở 2 mặt đáy là hai tam giác bằng nhau.
Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy. Khẳng định nào sau đây đúng?
SO ^ AC.
SA ^ AC.
SO ^ SC.
SA ^ AB.
Cho hình lập phương ABCD.A'B'C'D'. Chọn khẳng định sai.
(ABCD) ^ (ABB'A').
(ABCD) ^ (ABC'D').
(ABCD) ^ (CDD'C').
(ABCD) ^ (C'D'B'A').
Chọn khẳng định đúng?
Hình lăng trụ có các cạnh bên vuông góc với mặt đáy là hình lăng trụ đứng.
Hình lăng trụ có các cạnh bên song song với mặt đáy là hình lăng trụ đứng.
Các mặt bên hình lăng trụ đứng là tam giác đều.
Các mặt bên của hình lăng trụ đứng là tam giác.
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng AB và A'C' bằng
60°.
45°.
90°.
30°.
Cho hình lập phương (như hình vẽ). Đường vuông góc chung của hai đường thẳng chéo nhau CD và AA' là 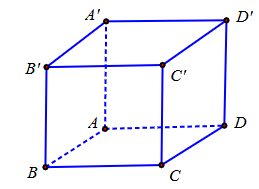
BB'.
AD.
CA.
CC'.
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Tính khoảng cách từ A' đến mặt phẳng (ABCD) biết AA' = a.
a.
2a.
3a.
\(\frac{a}{2}\).
Cho khối chóp diện tích đáy bằng S và chiều cao h. Khi đó thể tích V của khối chóp bằng:
\(V = \frac{1}{2}S.h\).
\(V = \frac{1}{3}S.h\).
V = S.h.
\(V = \frac{1}{6}S.h\).
Cho khối lăng trụ đứng tam giác ABC.A'B'C' có BB' = a. Đáy ABC là tam giác vuông cân tại B, \(AC = a\sqrt 2 \). Tính thể tích khối lăng trụ đã cho.
\(\frac{{{a^3}}}{3}\).
\(\frac{{{a^3}}}{6}\).
a3.
\(\frac{{{a^3}}}{2}\).
Cho khối chóp cụt có chiều cao h = 6, diện tích hai mặt đáy lần lượt là S = 4; S' = 16. Tính thể tích khối chóp cụt đó.
\(\frac{{56}}{3}\).
168.
28.
56.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 4, cạnh bên bằng 2.
a) Chiều cao của khối lăng trụ bằng 4.
b) Thể tích khối lăng trụ bằng \(8\sqrt 3 \).
c) Khoảng cách giữa AA' và BC bằng \(2\sqrt 3 \).
d) [A', BC, A] = 60°.
Cho hình lập phương ABCD.A'B'C'D'.
a) BD // B'D'.
b) (AC, B'D') = 90°.
c) Tam giác ACD' đều.
d) (AC, A'B) = 30°.
Cho hình chóp tam giác đều S.ABC và G là trọng tâm tam giác ABC.
a) SG ^ (ABC).
b) (SA, (ABC)) = \(\widehat {SAB}\).
c) \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A] với M là trung điểm của BC.
d) Khoảng cách từ S đến mặt phẳng (ABC) bằng độ dài đoạn thẳng SG.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khi đó:
a) Hai đường thẳng AB và A'D' vuông góc với nhau.
b) Hai mặt phẳng (ABCD) và (BB'D'D) vuông góc với nhau.
c) Khoảng cách từ điểm B đến mặt phẳng (AA'C'C) bằng \(\frac{{a\sqrt 3 }}{2}\).
d) Khoảng cách giữa hai đường thẳng BD và A'C' bằng a.
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, \(AA' = \frac{{3a}}{2}\). Biết rằng hình chiếu vuông góc của A' lên (ABC) là H trung điểm của BC. Khi đó:
a) A'H là đường cao hình lăng trụ.
b) Tam giác A'HA vuông tại A'.
c) Đường cao của khối lăng trụ trên là \(\frac{{a\sqrt 6 }}{2}\).
d) Thể tích của khối lăng trụ là \(\frac{{{a^3}\sqrt {18} }}{{24}}\).
PHẦN II. TRẢ LỜI NGẮN
Cho hình lăng trụ đứng ABC.A'B'C' có AB = 13; AC = 14; BC = 15. Gọi H là hình chiếu vuông góc của A lên BC. Tính khoảng cách giữa hai đường thẳng AA' và BC.
Một khối gỗ dạng hình chóp tứ giác đều S.ABCD có cạnh đáy 8 cm, cạnh bên tạo với mặt phẳng đáy một góc α với \(\tan \alpha = \sqrt 2 \). Người thợ cắt khối chóp bởi một mặt phẳng song song với đáy và qua trung điểm một cạnh bên để được một hình chóp S.A'B'C'D' và một hình chóp cụt đều ABCD.A'B'C'D'. Gọi V1 là thể tích của khối chóp S.A'B'C'D' và V2 là thể tích khối chóp cụt đều ABCD.A'B'C'D'. Biết \(\frac{{{V_1}}}{{{V_2}}} = \frac{a}{b}\) với a, b Î ℤ và \(\frac{a}{b}\) là phân số tối giản. Tính 2a + 3b.
Cho lăng trụ đứng ABC.MNK có đáy là tam giác đều cạnh 2. Đường thẳng MB hợp với đáy một góc 60°. Tính thể tích V của khối lăng trụ ABC.MNK.
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều như hình vẽ. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 4 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị triệu đồng.
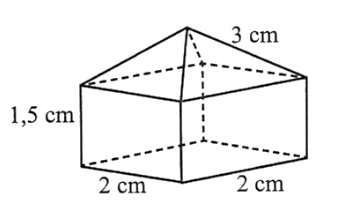
Người ta thiết kế một thiết bị kim loại có dạng như hình dưới (giá tiền mua kim loại là 2500 đồng/cm3). Thiết bị gồm 2 phần, phần dưới là khối lăng trụ tứ giác đều, phần trên là khối chóp tứ giác đều. Số tiền mua kim loại dùng để làm thiết bị đó là bao nhiêu nghìn đồng (kết quả làm tròn đến hàng đơn vị).