20 câu trắc nghiệm Toán 11 Cánh diều Bài 5. Khoảng cách (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong mặt phẳng (α), cho tam giác ABC vuông tại A có AB = 3a và AC = 4a. Khoảng cách từ điểm B đến đường thẳng AC bằng
4a.
5a.
a.
3a.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = 3a. Biết SA vuông góc với mặt phẳng đáy và SA = 5a. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng
3a.
2a.
\(a\sqrt {13} \).
5a.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a. Biết SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ đường thẳng BC đến mặt phẳng (SAD) bằng
a.
2a.
\(a\sqrt 5 \).
\(\frac{{2a}}{{\sqrt 5 }}\).
Cho tứ diện ABCD. Bốn điểm phân biệt M, N, P, Q lần lượt là hình chiếu vuông góc của A lên BC, CD, BD, (BCD). Khoảng cách từ điểm A đến đường thẳng CD bằng
AM.
AN.
AP.
AQ.
Cho hình chóp tứ giác S.ABCD. Bốn điểm phân biệt M, N, P, Q lần lượt là hình chiếu vuông góc của A lên các mặt phẳng (SBC), (SCD), (SBD), (BCD). Khoảng cách từ điểm A đến mặt phẳng (SBD) bằng
AM.
AN.
AP.
AQ.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = a, \(AC = a\sqrt 3 \), SA vuông góc với mặt phẳng đáy và SA = 2a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
\(\frac{{a\sqrt {57} }}{{19}}\).
\(\frac{{2a\sqrt {57} }}{{19}}\).
\(\frac{{2a\sqrt 3 }}{{19}}\).
\(\frac{{2a\sqrt {38} }}{{19}}\).
Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = a; BC = 2a, cạnh bên SA vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng SA và CD.
\(a\sqrt 6 \).
\(a\sqrt 5 \).
a.
2a.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng SA và BC.
\(a\sqrt 3 \).
a.
\(\frac{{a\sqrt 3 }}{4}\).
\(\frac{{a\sqrt 3 }}{2}\).
Cho hình chóp S.ABCD có SA ^ (ABCD), đáy ABCD là hình thang vuông có chiều cao AB = a. Gọi I và J lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa đường thẳng IJ và (SAD).
\(\frac{{a\sqrt 3 }}{3}\).
\(\frac{a}{2}\).
\(\frac{{a\sqrt 2 }}{2}\).
\(\frac{a}{3}\).
Cho hình lăng trụ ABC.A'B'C' có (A'ABB') ^ (ABC), AA' = 2a, \(\widehat {A'AB} = 60^\circ \). Tính khoảng cách giữa hai mặt phẳng (ABC) và (A'B'C').
\(\frac{{a\sqrt 3 }}{3}\).
\(a\sqrt 3 \).
\(\frac{{a\sqrt 2 }}{2}\).
\(a\sqrt 2 \).
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hình chóp S.ABCD có SA ^ (ABCD) và đáy ABCD là hình vuông tâm O.
a) SA ^ CD.
b) d(D, (SAC)) = DO.
c) (CD, (SAD)) = \(\widehat {CSD}\).
d) d(CD, SB) = BD.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết SA vuông góc với mặt phẳng đáy và \(SA = a\sqrt 3 \). Vẽ đường cao AH của tam giác SAB. Vẽ đường cao AK của tam giác SAD. Khi đó:
a) BC ^ AH.
b) Khoảng cách từ A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{2}\).
c) Khoảng cách từ A đến mặt phẳng (SBD) bằng \(\frac{{a\sqrt 2 }}{7}\).
d) Khoảng cách từ C đến mặt phẳng (AHK) bằng \(\frac{{a\sqrt 5 }}{5}\).
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật với AB = a; \(AD = a\sqrt 3 \), tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AB.
a) d(A, (SBD)) = \(\frac{{a\sqrt 6 }}{2}\).
b) \(d(SH,CD) = a\sqrt 3 \).
c) \(d(BC,SD) = \frac{{a\sqrt 3 }}{4}\).
d) \(d\left( {SB,CD} \right) = a\sqrt 3 \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a\sqrt 2 \), \(AC = a\sqrt 3 \). Cạnh bên \(SA = 2a\) và vuông góc với mặt đáy \((ABCD)\). Khi đó:
a) d(S, (ABCD)) = 2a.
b) \(AD//(SBC)\).
c) Khoảng cách từ \(D\) đến mặt phẳng \((SBC)\) bằng: \(\frac{{a\sqrt 3 }}{3}\).
d) Khoảng cách giữa hai đường thẳng \(SD,AB\) bằng: \(\frac{{2a\sqrt 5 }}{5}\).
Cho hình chóp S.ABC có SA ^ (ABC), tam giác ABC vuông tại B.
a) Khoảng cách từ C đến mặt phẳng (SAB) là đoạn BC.
b) BC ^ (SAB).
c) Khoảng cách từ B đến mặt phẳng (SAC) là đoạn AB.
d) SB ^ BC.
PHẦN II. TRẢ LỜI NGẮN
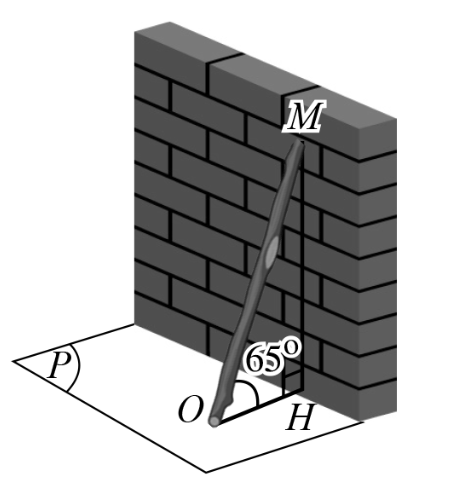
Hình bên dưới minh họa hình ảnh một chiệc gậy dài 3m đặt dựa vào tường, góc nghiêng giữa chiếc gậy và mặt đất là 65°. Đầu trên của chiếc gậy đặt vào vị trí M của tường. Tính khoảng cách từ vị trí M đến mặt đất (làm tròn đến hàng phần mười của mét).
Cho hình chóp S.ABC có mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông tại S, AB = 1; \(SA = \frac{3}{5}\). Khoảng cách từ điểm S đến mặt phẳng (ABC) là \(\frac{a}{b}\) (\(\frac{a}{b}\) là phân số tối giản). Tính a + b.
Cho hình hộp ABCD.A'B'C'D' có ABCD là hình thoi cạnh 1, AA' ^ (ABCD), AA' = 2; AC = 1. Tính khoảng cách giữa hai mặt phẳng (ABB'A') và (CDD'C') (kết quả làm tròn đến hàng phần trăm).
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, SAB là tam giác đều, (SAB) ^ (ABCD), AB = 1, AD = 2. Tính khoảng cách giữa BC và mặt phẳng (SAD) (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh bằng 2, các cạnh bên bằng \(2\sqrt 2 \), SO ^ (ABCD) . Tính khoảng cách giữa hai đường thẳng AB và SD (kết quả làm tròn đến hàng phần chục).
