20 câu Trắc nghiệm Toán 11 Cánh diều Bài 4. Hai mặt phẳng song song (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Hai mặt phẳng được gọi là song song với nhau nếu
chúng không có điểm chung.
chúng có một đường thẳng chung.
chúng có đúng một điểm chung.
chúng có ít nhất một điểm chung.
Mệnh đề nào sau đây là sai?
Qua một điểm bất kỳ có một và chỉ một mặt phẳng song song với một mặt phẳng cho trước.
Hai mặt phẳng được gọi là song song với nhau nêu chúng không có điểm chung.
Ba mặt phẳng phân biệt đôi một song song với nhau chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
Hai mặt phẳng song song cắt mặt phẳng thứ ba theo hai giao tuyến song song với nhau.
Cho mặt phẳng (P) chứa hai đường thẳng a, b và mặt phẳng (Q) chứa đường thẳng c. Mệnh đề nào sau đây là đúng?
Nếu a // c thì (P) // (Q).
Nếu b // c thì (P) // (Q).
Nếu a // (Q) và b // (Q) thì (P) // (Q).
Nếu a, b cắt nhau, a // (Q) và b // (Q) thì (P) // (Q).
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C sao cho \(\frac{{AB}}{{BC}} = \frac{2}{5}\) và đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A', B', C'. Tỉ số \(\frac{{A'B'}}{{B'C'}}\) bằng
\(\frac{2}{5}\).
\(\frac{2}{3}\).
\(\frac{5}{2}\).
\(\frac{1}{3}\).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA, AD. Mặt phẳng (MNO) song song với mặt phẳng nào sau đây?
(SAD).
(SAB).
(SBC).
(SCD).
Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Chọn khẳng định đúng trong các khẳng định sau:
(MNP) // (SBC).
(MNP) // (SAB).
(MNP) // (SAC).
(MNP) // (ABC).
Cho hình chóp S.ABCD, có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SB, SC, biết rằng (OMN) // (SAD). Khẳng định nào sau đây đúng?
(OMN) (SCD) = NQ // SD với Q CD.
(OMN) (SCD) = NA.
(OMN) (SCD) = NO.
(OMN) (SCD) = OD.
Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của SA, AB, AC, I là điểm trên cạnh AB thỏa mãn AB = 4AI. Mặt phẳng (MPI) song song với mặt phẳng nào sau đây?
(SBC).
(SCN).
(SAB).
(ABC).
Cho hình chóp S.ABCD có đáy ABCD là hình thang, biết MA = MB, CD = 2ND và P là trung điểm của SC. Mặt phẳng (MNP) song song với mặt phẳng nào sau đây?
(SAB).
(SAD).
(SBC).
(SBC).
(SAC).
Cho hình tứ diện ABCD. Gọi I, J, K lần lượt là trọng tâm của các tam giác ABD, ACD, ABC và M, N,P lần lượt là trung điểm của các cạnh BD, CD, BC. Khẳng định nào sau đây là đúng?
(DJK) // (ABC).
(IJK) // (BCD).
(KMN) // (ABC).
(IJK) // (AMD).
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD. M, N, P lần lượt là trung điểm của SB, SD, SC. Khi đó
a) Tỉ số đồng dạng của tam giác OMP và tam giác SDA là \(\frac{1}{3}\).
b) Đường thẳng MN song song với đường thẳng BC.
c) Đường thẳng OP song song với mặt phẳng (SAD).
d) Mặt phẳng (MOP) song song với mặt phẳng (SAD).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SB, BC.
a) Đường thẳng AB song song với đường thẳng CD.
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là đường thẳng qua S và song song với AC.
c) Đường thẳng CD song song với mặt phẳng (OMN).
d) Hai mặt phẳng (SAD) và (OMN) song song.
Cho hình chóp S.ABCD có đáy ABCD là hình thang (với AD // BC). Gọi M, N là trung điểm của SA, SD; P là điểm trên cạnh SC sao cho SP = 3PC và I = MP AC.
a) Giao tuyến của mặt phẳng (MNP) và (ABCD) là đường thẳng đi qua I và song song với AD.
b) MN // (ABCD).
c) (MNP) // (ABCD).
d) I là giao điểm của đường thẳng MP và (ABCD).
Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD) // (EFMH), CK // DH. Khối gỗ bị hỏng một góc như hình minh họa phía dưới. Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (α) đi qua điểm K và song song với mặt phẳng (ABCD).
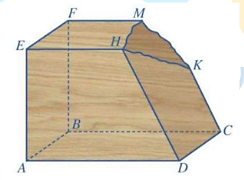
Biết CK =80 cm, DH = 128 cm, BF = 1 m. Giả sử (α) cắt BF tại I. Tính độ dài đoạn BI (theo đơn vị cm).
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Biết AB = 5a, CD = 2a. Gọi E là điểm thuộc cạnh SB thỏa mãn \(\frac{{ES}}{{EB}} = \frac{m}{n}\) với \(\frac{m}{n}\) là phân số tối giản. Biết CE song song với mặt phẳng (SAD). Tính 2m + 3n.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M là trọng tâm của tam giác ABE. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AFD). Mặt phẳng (P) cắt đường thẳng AC tại N. Tính \(\frac{{AN}}{{NC}}\).
Cho hình chóp S.ABCD có đáy là hình thang, AD // BC, AD = xBC. Gọi M, N lần lượt là 2 điểm nằm trên AD, SD thỏa mãn \(\frac{{AM}}{{AD}} = \frac{{SN}}{{SD}} = \frac{1}{3}\). Để (CMN) // (SAB) thì khi đó giá trị x bằng bao nhiêu?
Cho hình chóp S.ABC có G là trọng tâm tam giác ABC. Mặt phẳng (α) đi qua G và song song với mặt phẳng (SBC), M là giao điểm của (α) với SA. Tính \(\frac{{SM}}{{SA}}\) (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Khi đó:
a) Mặt phẳng (MNP) cắt SD tại Q. Khi đó NQ = a.
b) (MNO) // (SCD).
c) (MNP) // (ABCD).
d) Diện tích của tứ giác MNPQ bằng a2.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi H, I, K lần lượt là trung điểm của SA, SB, SC. Gọi M là giao điểm của AI và KD, N là giao điểm của DH và CI. Khi đó:
a) HI // (ABCD).
b) (HIK) // (ABCD).
c) Tứ giác ABMS là hình bình hành.
d) (SMN) cắt (HIK).
