20 câu Trắc nghiệm Toán 11 Cánh diều Bài 3. Hàm số liên tục (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Chọn đáp án đúng
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại một điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó là liên tục tại ba điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó là liên tục tại hai điểm của khoảng đó.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau: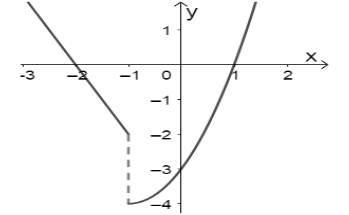
Hàm số f(x) liên tục trên ℝ.
Hàm số f(x) liên tục tại x = 1.
Hàm số f(x) liên tục tại x = −1.
Hàm số f(x) liên tục trên khoảng (−3; 1).
Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K. Hàm số y = f(x) liên tục tại điểm x0 khi nào?
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không tồn tại.
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\).
f(x0) không tồn tại.
Cho hàm số \(f\left( x \right) = \frac{1}{x}\). Khi đó
f(x) liên tục trên (−∞; 1).
f(x) liên tục trên (−∞; +∞).
f(x) liên tục trên (−1; +∞).
f(x) liên tục trên (−∞; 0) và (0; +∞).
Hàm số \(y = \frac{1}{{{x^2} - 3x + 2}}\) liên tục trên khoảng nào dưới đây?
(1; 2).
(−1; 2).
(−∞; 2).
(1; +∞).
Hàm số nào sau đây gián đoạn tại x = 1?
\(y = \frac{{{x^2} + 2x - 1}}{{x + 1}}\).
\(y = \frac{{2x + 1}}{{{x^2} + 1}}\).
y = x3 + x + 1.
\(y = \frac{{x + 3}}{{{x^2} - 1}}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{x - 2}}{{\sqrt {x + 2} - 2}}\;\;khi\;x \ne 2\\4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;x = 2\end{array} \right.\). Chọn mệnh đề đúng?
Hàm số liên tục tại x = 2.
Hàm số gián đoạn tại x = 2.
f(4) = 2.
\(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 2\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {1 + 2x} - 1}}{x}\;\;khi\;x > 0\\x + 2021\;\;\;\;\;\;khi\;x \le 0\end{array} \right.\). Mệnh đề nào sau đây đúng?
Hàm số liên tục trên ℝ.
Hàm số gián đoạn tại x = 3.
Hàm số gián đoạn tại x = 0.
Hàm số gián đoạn tại x = 1.
Hàm số nào dưới đây liên tục trên tập ℝ.
\(f\left( x \right) = \frac{{x + 1}}{{{x^2}}}\).
\(f\left( x \right) = \frac{{x - 2}}{{x - 3}}\).
f(x) = x2 + 2x + 1.
\(f\left( x \right) = \sqrt {4 - {x^2}} \).
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{5x - {x^2}}}{{\sqrt {{x^4} + 4{x^2}} }}\;\;khi\;x < 0\\m + \frac{{2x - 3}}{{x + 2}}\;\;\;\;\;khi\;x \ge 0\end{array} \right.\) liên tục tại điểm x0 = 0.
m = −1.
m = 4.
\(m = \frac{1}{2}\).
m = −3.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(f\left( x \right) = \frac{{2{x^2} - 5x + 2}}{{{x^2} - 4}}\).
a) Hàm số f(x) liên tục trên khoảng (3; +∞).
b) Hàm số f(x) liên tục tại x = −2.
c) Hàm số f(x) gián đoạn tại x = 2.
d) Nếu \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \frac{a}{b}\) với a, b Î ℤ; \(\frac{a}{b}\) tối giản thì a2 + b2 = 25.
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}} & {\rm{khi}}\,x \ne 1\\x + 1 & {\rm{khi}}\,x = 1\end{array} \right.\) và \(g(x) = 4{x^2} - x + 1\). Khi đó:
a) Ta có \(f(1) = 2\).
b) Hàm số \(f\left( x \right)\) liên tục tại điểm \({x_0} = 1\).
c) Hàm số \(g\left( x \right)\)liên tục tại điểm \({x_0} = 1\).
d) Hàm số \(y = f\left( x \right) - g\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {x + 2} - 2}}{{2 - x}}\;\;khi\;x > 2\\\frac{{1 - x}}{4}\;\;\;\;\;\;\;\;\;\;\;khi\;x \le 2\end{array} \right.\). Khi đó
a) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = - \frac{1}{4}\).
b) \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \frac{1}{4}\).
c) Hàm số f(x) gián đoạn tại điểm x0 = 2.
d) Hàm số f(x) liên tục trên khoảng (−∞; 2).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^2} - 4x + 4} }}{x}\;\;khi\; < 2\\m{x^2} - 3\;\;\;\;\;\;\;\;\;\;khi\;x \ge 2\end{array} \right.\) (m là tham số).
a) Khi m = 1 thì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\).
b) Hàm số f(x) liên tục tại x = 2 khi m = 1.
c) f(2) = 4m – 3.
d) \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 1\).
Cho hàm số \(y = f\left( x \right) = \frac{{3x + 1}}{{x - 1}}\). Khi đó:
a) \[\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = + \infty \].
b) \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 4\).
c) Hàm số y = f(x) liên tục tại điểm x0 = 1.
d) Hàm số y = f(x) liên tục trên từng khoảng (−∞; 1) và (1; +∞).
PHẦN II. TRẢ LỜI NGẮN
Hãng taxi Xanh SM đưa ra giá cước dựa trên số quãng đường di chuyển cho bởi hàm T(x) đồng khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:
\(T\left( x \right) = \left\{ \begin{array}{l}1500\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;0 < x \le 1\\a + \left( {x - 1} \right).14000\;\;\;\;\;khi\;1 < x \le 20\\b + \left( {x - 20} \right).12000\;\;khi\;x > 20\end{array} \right.\). Biết rằng tiền cước được cho bởi hàm liên tục khi đó \(\frac{b}{a}\) bằng bao nhiêu (kết quả làm tròn đến hàng phần mười)?
Tìm giá trị của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {2x - 1} - 1}}{{x - 1}}\;\;khi\;x \ne 1\\m - 2024\;\;\;\;\;khi\;x = 1\end{array} \right.\) liên tục tại x = 1.
Biết hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3x + b\;\;khi\;x \le - 1\\x + a\;\;\;\;khi\;x > - 1\end{array} \right.\) liên tục tại x = −1. Tìm a – b.
Tìm giá trị của m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - x - 2}}{{x - 2}}\;khi\;x \ne - 2\\m\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;x = - 2\end{array} \right.\) liên tục trên tập xác định của chúng.
Một chất điểm chuyển động với tốc độ được cho bởi hàm số \(v\left( t \right) = \left\{ \begin{array}{l}10 + a\;\;\;\;\;\;\;\;khi\;0 \le t \le 5\\{t^2} - 5t + 10\;khi\;t > 5\end{array} \right.\), trong đó v(t) được tính theo đơn vị m/s và t được tính theo giây. Tìm a để hàm v(t) có liên tục tại điểm t = 5.
