10 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Chọn đáp án đúng
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại một điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó là liên tục tại ba điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó là liên tục tại hai điểm của khoảng đó.
Cho hàm số y = f(x) có đồ thị như hình vẽ. Chọn khẳng định đúng trong các khẳng định sau:
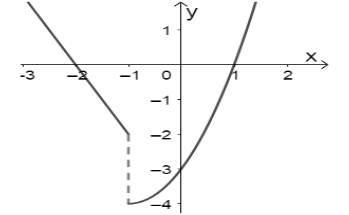
Hàm số f(x) liên tục trên ℝ.
Hàm số f(x) liên tục tại x = 1.
Hàm số f(x) liên tục tại x = −1.
Hàm số f(x) liên tục trên khoảng (−3; 1).
Cho hàm số y = f(x) xác định trên khoảng K và x0 ∈ K. Hàm số y = f(x) liên tục tại điểm x0 khi nào?
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không tồn tại.
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\).
f(x0) không tồn tại.
Cho hàm số \(f\left( x \right) = \frac{1}{x}\). Khi đó
f(x) liên tục trên (−∞; 1).
f(x) liên tục trên (−∞; +∞).
f(x) liên tục trên (−1; +∞).
f(x) liên tục trên (−∞; 0) và (0; +∞).
Hàm số \(y = \frac{1}{{{x^2} - 3x + 2}}\) liên tục trên khoảng nào dưới đây?
(1; 2).
(−1; 2).
(−∞; 2).
(1; +∞).
Hàm số nào sau đây gián đoạn tại x = 1?
\(y = \frac{{{x^2} + 2x - 1}}{{x + 1}}\).
\(y = \frac{{2x + 1}}{{{x^2} + 1}}\).
y = x3 + x + 1.
\(y = \frac{{x + 3}}{{{x^2} - 1}}\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{x - 2}}{{\sqrt {x + 2} - 2}}\;\;khi\;x \ne 2\\4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;khi\;x = 2\end{array} \right.\). Chọn mệnh đề đúng?
Hàm số liên tục tại x = 2.
Hàm số gián đoạn tại x = 2.
f(4) = 2.
\(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 2\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {1 + 2x} - 1}}{x}\;\;khi\;x > 0\\x + 2021\;\;\;\;\;\;khi\;x \le 0\end{array} \right.\). Mệnh đề nào sau đây đúng?
Hàm số liên tục trên ℝ.
Hàm số gián đoạn tại x = 3.
Hàm số gián đoạn tại x = 0.
Hàm số gián đoạn tại x = 1.
Hàm số nào dưới đây liên tục trên tập ℝ.
\(f\left( x \right) = \frac{{x + 1}}{{{x^2}}}\).
\(f\left( x \right) = \frac{{x - 2}}{{x - 3}}\).
f(x) = x2 + 2x + 1.
\(f\left( x \right) = \sqrt {4 - {x^2}} \).
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{5x - {x^2}}}{{\sqrt {{x^4} + 4{x^2}} }}\;\;khi\;x < 0\\m + \frac{{2x - 3}}{{x + 2}}\;\;\;\;\;khi\;x \ge 0\end{array} \right.\) liên tục tại điểm x0 = 0.
m = −1.
m = 4.
\(m = \frac{1}{2}\).
m = −3.
