20 câu trắc nghiệm Toán 11 Cánh diều Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Trong các mệnh đề sai, mệnh đề nào đúng?
Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và đường thẳng b với b vuông góc với (P).
Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a song song với b.
Cho tứ diện ABCD có AB, BC, BD đôi một vuông góc với nhau. Khẳng định nào dưới đây đúng?
Góc giữa CD và mặt phẳng (ABD) là góc \(\widehat {CBD}\).
Góc giữa AC và mặt phẳng (BCD) là góc \(\widehat {ACB}\).
Góc giữa AD và mặt phẳng (ABC) là góc \(\widehat {ADB}\).
Góc giữa AC và mặt phẳng (ABD) là góc \(\widehat {CBA}\).
Cho hình chóp S.ABC có SB ^ (ABC). Góc giữa SC và (ABC) là góc giữa
SC và AC.
SC và AB.
SC và BC.
SC và SB.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Số đo của góc giữa SA và (ABC).
30°.
45°.
60°.
75°.
Cho hình chóp S.ABC có SA ^ (ABC), \(SA = 2a\sqrt 3 ,AB = 2a\), tam giác ABC vuông cân tại B. Gọi M là trung điểm của SB. Góc giữa đường thẳng CM và mặt phẳng (SAB) bằng
30°.
45°.
60°.
90°.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B. Cạnh bên SA vuông góc với mặt phẳng đáy. Gọi I là trung điểm của BC. Góc nhị diện [S, BC, A] là
\(\widehat {SIA}\).
\(\widehat {SBA}\).
\(\widehat {SCA}\).
\(\widehat {ASB}\).
Cho hình chóp S.ABCD với đáy là hình vuông tâm O, cạnh 2a, \(SA = a\sqrt 6 \) và vuông góc với đáy. Góc nào dưới đây là góc phẳng nhị diện của góc nhị diện [S, BD, A].
\(\widehat {ADS}\).
\(\widehat {ABS}\).
\(\widehat {SCA}\).
\(\widehat {SOA}\).
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt phẳng đáy. Tính số đo góc nhị diện [B, SA, D].
45°.
90°.
60°.
30°.
Cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc và SA = SB = SC = 1. Tính cosα, trong đó α là góc nhị diện [S, BC, A].
\(\cos \alpha = \frac{1}{{\sqrt 2 }}\).
\(\cos \alpha = \frac{1}{{2\sqrt 3 }}\).
\(\cos \alpha = \frac{1}{{3\sqrt 2 }}\).
\(\cos \alpha = \frac{1}{{\sqrt 3 }}\).
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SC ^ (ABCD), CD = 4a; \(SC = \sqrt 5 a\). Số đo góc phẳng nhị diện [C, DA, S] gần nhất với kết quả
29,21°.
41,01°.
34,01°.
45,81°.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Một tấm cầu dốc kê bậc thềm được làm bằng cao su như hình vẽ sau. Biết BA, ED cùng vuông góc với (ACFD), BCFE là hình vuông có cạnh bằng 1m và AB = 0,3m như hình vẽ.
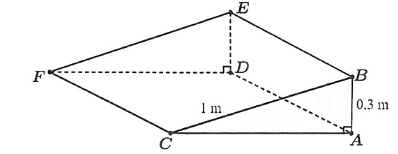
a) Góc giữa đường thẳng CB và mặt phẳng (ACFD) là góc \(\widehat {BCA}\).
b) Góc giữa đường thẳng AB và mặt phẳng (ACFD) bằng 90°.
c) Góc giữa đường thẳng CB và mặt phẳng (ACFD) bằng 30°.
d) Góc giữa đường thẳng BF và mặt phẳng (ACFD) bằng 15°.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 2a. Khi đó:
a) (CD, SA) = 45°.
b) AD ^ (SAB).
c) (SC, (ABCD)) = 45°.
d) Số đo của góc nhị diện [B, SA, D] bằng 90°.
Cho hình chóp S.ABCD có SA ^ (ABCD), ABCD là hình thoi cạnh a, AC = a, \(SA = \frac{a}{2}\). Khi đó:
a) BD ^ (SAC).
b) Góc giữa SD và (ABCD) là \(\widehat {ASD}\).
c) Góc giữa SD và (ABCD) nhỏ hơn 30°.
d) Số đo của góc nhị diện [S, CD, A] bằng 30°.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SA vuông góc với mặt phẳng (ABCD), SA = a, AB = a, AD = 2a. Khi đó:
a) \(\widehat {SOA}\) là góc phẳng nhị diện của góc [S, BD, A].
b) Số đo của góc nhị diện [A, BC, S] bằng 45°.
c) \(\widehat {SCA}\) là góc phẳng nhị diện của góc [S, CD, A].
d) Số đo của góc nhị diện [S, AB, D] bằng 90°.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\)vuông góc với mặt phẳng đáy và \(SA = a\sqrt 2 \).
a) \(AB\) là hình chiếu của \(SB\) trên mặt phẳng \((ABCD)\).
b) \((SB,(ABCD)) \approx 54,74^\circ \).
c) \((SC,(ABCD)) = 45^\circ \).
d) \((SC,(SAB)) = 60^\circ \).
PHẦN II. TRẢ LỜI NGẮN
Hai vách ngăn bàn làm việc trong hình dưới đây cắt nhau tạo thành bốn góc nhị diện. Số đo của các góc nhị diện là bao nhiêu độ?

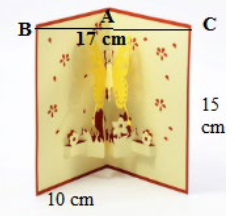
Trong hình dưới đây, tấm thiệp được mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của tấm thiệp. Tính độ mở của tấm thiệp (kết quả làm tròn đến hàng đơn vị).
Cho hình vuông ABCD tâm O, cạnh bằng 2. Trên đường thẳng qua O vuông góc với (ABCD) lấy điểm S. Biết góc giữa SA và mặt phẳng (ABCD) có số đo bằng 45°. Tính độ dài SO (kết quả làm tròn đến hàng phần mười).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 ,SA \bot \left( {ABCD} \right)\). Góc giữa đường thẳng SD và mặt phẳng (ABCD) là α°. Tìm α.
Cho hình chóp S.ABCD có đáy là hình thoi tâm I, cạnh a và có \(\widehat {BAD} = 60^\circ \). Các cạnh bên \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\). Gọi φ là góc nhị diện [S, BD, A]. Giá trị tanφ bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
