20 câu Trắc nghiệm Toán 11 Cánh diều Bài 3. Cấp số nhân (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Dãy số nào dưới đây không phải là cấp số nhân?
1; −3; 9; −27; 54.
1; 2; 4; 8; 16.
1; −1; 1; −1; 1.
1; −2; 4; −8; 16.
Dãy số nào dưới đây là một cấp số nhân
1; 2; 3; 4; 5.
1; 3; 6; 9; 12.
2; 4; 6; 8; 10.
2; 2; 2; 2; 2.
Trong các dãy số (un) sau, dãy số nào là cấp số nhân?
un = 5n.
un = 1 + 5n.
un = 5n + 1.
un = 5 + n2.
Cho cấp số nhân (un) có u1 = 3 và u2 = 9. Công bội của cấp số nhân bằng
−6.
3.
\(\frac{1}{3}\).
6.
Cho cấp số nhân (un) với u1 = 3 và công bội q = 2. Giá trị của u2 bằng
8.
9.
\(\frac{3}{2}\).
6.
Cho cấp số nhân (un) có u5 = 2 và u9 = 6. Tính u21.
18.
54.
162.
486.
Cho dãy số 4; 12; 36; 108; 324; ... . Số hạng thứ 10 của dãy số đó là
73872.
77832.
72873.
78732.
Cho cấp số nhân (un) có u1 = 3 và q = −2. Tổng 10 số hạng đầu tiên của cấp số nhân đó bằng
S10 = −511.
S10 = −1023.
S10 = 1025.
S10 = −1025.
Cho cấp số nhân (un) có \({u_1} = \frac{1}{3}\) và u8 = 729. Tổng 8 số hạng đầu tiên của cấp số nhân đó bằng
\(\frac{{1 - {3^8}}}{2}\).
\(\frac{{{3^8} - 1}}{6}\).
\(\frac{{{3^8} - 1}}{2}\).
\(\frac{{1 - {3^8}}}{6}\).
Người ta thiết kế một cái tháp 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp. Biết đế tháp có diện tích là 12288 m2. Tính diện tích mặt trên cùng
8 m2.
6 m2.
10 m2.
12 m2.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho dãy số (an) xác định bởi hệ thức truy hồi a1 = 2; an + 1 = −2an với n Î ℕ*.
a) (an) là một cấp số nhân với a1 = 2 và q = −2.
b) Số hạng thứ 8 của dãy bằng 256.
c) Số −2048 là một số hạng của dãy.
d)S10 = −682.
Cho cấp số nhân (un) có số hạng đầu bằng −2 và công bội bằng 2.
a) u5 = −32.
b) S3 = −8.
c) Số −50 là một số hạng của cấp số nhân (un).
d) \(\frac{{{S_4}}}{{{S_3}}} = {u_4}\).
Cho cấp số nhân (un) có u1 = 2; u2 = −4.
a) Công bội q = 2.
b) u5 = −32.
c) Số −64 là số hạng thứ 6 của (un).
d) Tổng của 8 số hạng đầu tiên của cấp số nhân bằng −170.
Tương truyền rằng nhà vua Ấn Độ cho phép người phát minh ra bàn cờ vua được lựa chọn phần thưởng tùy theo sở thích. Người đó xin nhà vua: “Bàn cờ có 64 ô với ô thứ nhất thần xin nhận 1 hạt thóc, ô thứ hai thì gấp đôi ô đầu, ô thứ ba thì lại gấp đôi ô thứ hai, … cứ như vậy ô sau nhận số hạt thóc gấp đôi phần thưởng dành cho ô liền trước và thần xin nhận tổng số các hạt thóc ở 64 ô”. Biết rằng khối lượng của 100 hạt thóc là 20 gam.
a) Số hạt thóc ở 64 ô là một cấp số nhân có u1 = 1; q = 2.
b) Số hạt thóc ở ô thứ tám là 28.
c) Tổng khối lượng thóc của 64 ô trên bàn cờ là 364 tỉ tấn.
d) Giả sử người đó muốn chở số thóc ở trên 32 ô đầu tiên về bằng tàu thủy, biết rằng mỗi chuyến tàu chở tối đa 10 tấn hàng hóa. Khi đó, người đó cần tối thiểu 85 chuyến tàu để chở hết số thóc đó.
Cho dãy số (un) với \(\left\{ \begin{array}{l}{u_1} = 3\\{u_n} = 3{u_{n - 1}}\end{array} \right.\).
a) Ba số hạng đầu của dãy là 3; 9; 26.
b) Dãy (un) là cấp số nhân với công bội bằng 3.
c) Số hạng thứ 10 của dãy số này là u10 = 59049.
d) Tổng 11 số hạng đầu của dãy số trên là 88572.
PHẦN II. TRẢ LỜI NGẮN
Viết thêm bốn số vào giữa hai số 160 và 5 để được một cấp số nhân gồm sáu số hạng. Tìm tổng tất cả các số hạng của cấp số nhân đó.
Tổng của chín số hạng đầu của cấp số nhân 20; 10; 5; … với kết quả làm tròn đến hàng phần mười.
Cho cấp số nhân (un) với số hạng đầu u1 = −5, công bội q = 2. Số −320 là số hạng thứ bao nhiêu của cấp số nhân trên?
Do ảnh hưởng của dịch Covid 19 nên doanh thu 6 tháng đầu năm của công ty A không đạt kế hoạch. Cụ thể, doanh thu 6 tháng đầu năm đạt 20 tỷ đồng, trong đó tháng 6 đạt 6 tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty đưa ra chỉ tiêu: kể từ tháng 7 mỗi tháng phải tăng doanh thu so với tháng kề trước 10%. Hỏi theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là bao nhiêu tỷ đồng (làm tròn đến một chữ số thập phân).
Cho hình vuông ABCD có cạnh bằng 16 và có diện tích S1. Nối 4 trung điểm A1; B1; C1; D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100 (tham khảo hình bên dưới).
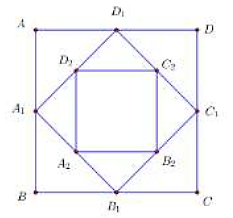
Biết tổng S = S1 + S2 + …+ S100 = \(\frac{{{2^a} - 1}}{{{2^b}}}\) (a, b Î ℕ). Tính a + b.

