20 câu Trắc nghiệm Toán 11 Cánh diều Bài 2. Hai đường thẳng song song trong không gian (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Trong các mệnh đề sau, mệnh đề nào đúng?
Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
Hai đường thẳng song song khi và chỉ khi chúng không có điểm chung.
Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Trong các mệnh đề sau, mệnh đề nào đúng?
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng nhau.
Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt phẳng song song.
Cho ba mặt phẳng phân biệt (α), (β), (γ) có (α) (β) = d1; (β) (γ) = d2; (α) (γ) = d3. Khi đó ba đường thẳng d1; d2; d3
Đôi một cắt nhau.
Đôi một song song.
Đồng quy.
Đôi một song song hoặc đồng quy.
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\). Gọi \(G\) là trọng tâm tam giác \(BCD\). Đường thẳng \(AG\) cắt đường thẳng nào trong các đường thẳng dưới đây?
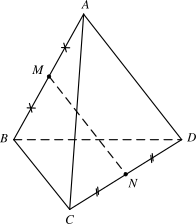
Đường thẳng \(MN\).
Đường thẳng \(CM\).
Đường thẳng \(DN\).
Đường thẳng \(CD\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(SA\) và \(SC\). Đường thẳng \(IJ\) song song với đường thẳng nào?
\(BC\).
\(AC\).
\(SO\).
\(BD\).
Cho hình chóp \(S.ABCD\) có đáy là hình thang đáy lớn là \(CD\). Gọi \(M\) là trung điểm của cạnh \(SA\), \(N\) là giao điểm của cạnh \(SB\) và mặt phẳng \(\left( {MCD} \right)\). Mệnh đề nào sau đây là mệnh đề đúng?
\[MN\] và \(SD\) cắt nhau.
\[MN//\,CD\].
\[MN\] và \(SC\) cắt nhau.
\[MN\] và \(CD\) chéo nhau.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SA (tham khảo hình vẽ). Giao tuyến của mặt phẳng (CMD) và mặt phẳng (SAB) là đường thẳng song song với đường thẳng nào dưới đây?
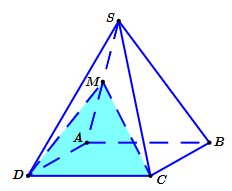
CM.
CD.
AD.
SB.
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, AD, CD, BC. Khẳng định nào sau đây sai?
MN // BD và \(MN = \frac{1}{2}BD\).
MN // PQ và MN = PQ.
Tứ giác MNPQ là hình bình hành.
MN chéo nhau với PQ.
Cho hình chóp S.ABCD có đáy ABCD là một hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND), I là giao điểm của AN và DP. Khẳng định nào sau đây là đúng?
SI trùng với CD.
SI song song với CD.
SI cắt với CD.
SI chéo với CD.
Cho tứ diện ABCD. Gọi I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) là đường thẳng:
qua I và song song với AB.
qua J và song song với BD.
qua G và song song với DC.
qua G và song song với BC.
Cho hình chóp S.ABCD có ABCD là hình bình hành. Khi đó:
a) SC và AB chéo nhau.
b) SA song song với BC.
c) SA cắt SC.
d) AB song song với CD.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, SC, SB.
a) MP // SA.
b) Giao điểm của đường thẳng MD với mặt phẳng (SBC) là giao điểm của đường thẳng DM với đường thẳng SB.
c) Nếu I là giao điểm của đường thẳng MD với mặt phẳng (SBD) thì M là trung điểm của đoạn thẳng ID.
d) Ba đường thẳng AN, DP, SO đồng quy.
Cho hình chóp S.ABCD có đáy là tứ giác lồi không có cặp cạnh song song. Gọi M, N lần lượt là trung điểm SA, SB và P = AC BD, d là giao tuyến giữa mặt phẳng (MNP) và mặt phẳng (ABCD).
a) Đường thẳng d đi qua điểm P và song song với đường thẳng CD.
b) Gọi E = d BC. Khi đó NE // SC.
c) Gọi F = d AD. Khi đó (SAD) (MNP) = MF.
d) Tứ giác MNEF là hình thang.
Cho hình chóp S.ABCD, có đáy ABCD là một hình bình hành tâm O. Gọi I, K lần lượt là trung điểm của SB và SD.
a) SO là giao tuyến của (SAC) và (SBD).
b) Giao điểm J của SA với (CKB) thuộc đường thẳng đi qua K và song song với DC.
c) Giao tuyến của (OIA) và (SCD) là đường thẳng đi qua C và song song với SD.
d) CD // IJ.
Cho hình chóp S.ABCD có đáy là hình bình hành. Điểm M thuộc cạnh SA, điểm E và F lần lượt là trung điểm của AB và BC.
a) EF // AC.
b) Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng qua S và song song với AC.
c) Giao tuyến của hai mặt phẳng (MBC) và (SAD) là đường thẳng qua M và song song với BC.
d) Giao tuyến của hai mặt phẳng (MEF) và (SAC) là đường thẳng qua M và song song với AC.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là điểm thuộc đoạn CD sao cho CE = 3ED. Gọi F là giao điểm của AD và mặt phẳng (MNE). Biết MN = 10. Tính độ dài đoạn EF.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là các điểm trên các đoạn SB, SC sao cho MS = 2MB, NS = NC. Mặt phẳng (AMN) cắt cạnh SD tại K. Tính diện tích của tứ giác BDKM khi biết tam giác SBD là tam giác đều có cạnh dài 6 cm (làm tròn kết quả đến hàng phần trăm).
Cho tứ diện ABCD, M là điểm thuộc BC sao cho MC = 2MB. Gọi N, P lần lượt là trung điểm của BD và AD. Điểm Q là giao điểm của AC và (MNP). Tính \(\frac{{QC}}{{QA}}\).
Cho các mệnh đề sau:
I) Hai đường thẳng song song với nhau thì đồng phẳng.
II) Hai đường thẳng không có điểm chung thì chéo nhau.
III) Hai đường thẳng chéo nhau thì không có điểm chung.
IV) Hai đường thẳng chéo nhau thì không đồng phẳng.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Hai điểm M, N theo thứ tự là trung điểm của các cạnh AB, SC. Gọi I, J theo thứ tự là giao điểm của AN, MN với mặt phẳng (SBD). Giá trị \(k = \frac{{IA}}{{IN}} + \frac{{JN}}{{JM}}\) bằng bao nhiêu?
