20 câu Trắc nghiệm Toán 11 Cánh diều Bài 1. Giới hạn của dãy số (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Cho hai dãy (un) và (vn) thỏa mãn limun = 6 và limvn = 12. Giá trị của lim(un – vn) bằng
2.
72.
18.
−6.
Cho hai dãy (un) và (vn) thỏa mãn \(\lim {u_n} = \sqrt 3 \) và limvn = 2. Giá trị của \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng
\(2\sqrt 3 \).
\(\frac{{\sqrt 3 }}{2}\).
\(2 + \sqrt 3 \).
\( - 2 + \sqrt 3 \).
Tính giới hạn \(I = \lim \frac{{2n + 2023}}{{3n + 2024}}\).
\(I = \frac{2}{3}\).
\(I = \frac{3}{2}\).
\(I = \frac{{2023}}{{2024}}\).
\(I = 1\).
Tính \(\lim \frac{{2{n^2} - 3}}{{{n^6} + 5{n^5}}}\).
2.
0.
\(\frac{{ - 3}}{5}\).
−3.
Giới hạn \(\lim \frac{{{3^n} + {2^n}}}{{{4^n}}}\) có kết quả là
0.
\(\frac{5}{4}\).
\(\frac{3}{4}\).
+∞.
Cho các dãy số (un), (vn) và limun = a, limvn = +∞ thì \(\lim \frac{{{u_n}}}{{{v_n}}}\) bằng
1.
0.
−∞.
+∞.
Cho số thập phân vô hạn tuần hoàn a = 2,151515... (chu kỳ 15), a được biểu diễn dưới dạng phân số tối giản, trong đó m, n là các số nguyên dương. Tìm tổng m + n.
m + n = 104.
m + n = 312.
m + n = 38.
m + n = 114.
Dãy số nào sau đây có giới hạn bằng 0?
\({u_n} = \frac{{3n}}{{2{n^2} + 1}}\).
un = 2n – 5n2.
\({u_n} = \frac{{5n + 1}}{{7n + 13}}\).
\({u_n} = \frac{{2{n^2} + 3n - 1}}{{{n^2} + 7n - 3}}\).
Tính giới hạn \(\lim \frac{{{{5.2}^{n + 2}} - {{2.3}^{n + 2}}}}{{7 + {3^{n + 1}}}}\) bằng
\( - \frac{2}{7}\).
\(\frac{5}{7}\).
6.
−6.
Tính \(\lim \left( {{n^5} - 3n + 2} \right)\).
1.
+∞.
−∞.
−1.
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Giả sử ta có \(\lim {u_n} = a\) và \(\lim {v_n} = b\) với a, b ∈ ℝ. Khi đó:
a) \(\lim \left( {{u_n}.{v_n}} \right) = a.b\).
b) \(\lim \left( {2{u_n} - {v_n}} \right) = 2a - b\).
c) \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\).
d) \(\lim \frac{{{u_n} + 2{v_n}}}{{{u_n}}} = \frac{a}{b}\) với a ≠ 0.
Biết \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = 2\) và \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = b\).
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) 2a – b = 0.
d) Ba số a, b, 16 lập thành một cấp số nhân.
Viết được các số thập phân vô hạn tuần hoàn dưới dạng phân số tối giản, ta được:
\(0,212121... = \frac{a}{b}\); \(4,333... = \frac{c}{d}\). Khi đó
a) a + b = 40.
b) Ba số a;b; 58 tạo thành một cấp số cộng.
c) c + d = 15.
d) limc = 13.
Cho hai dãy số (un) và (vn) có \({u_n} = \frac{1}{{n + 1}};{v_n} = \frac{3}{{n + 3}}\).
a)\(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{1}{3}\).
b) lim(vn + 1) = 1.
c) Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực, vì |un| có thể nhỏ hơn một số dương tùy ý, kể từ một số hạng nào đó trở đi.
d) lim(un – vn) = 0.
Cho hai dãy số (un), (vn) với un = 4.3n – 7n + 1 ; vn = 7n.
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{v_n}}} = 0\).
b)\(\mathop {\lim }\limits_{n \to + \infty } {v_n} = + \infty \).
c) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n} - {v_n}}}{{3{u_n} + 2{v_n}}} = \frac{8}{{19}}\).
d)\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \).
PHẦN II. TRẢ LỜI NGẮN
Tìm \(\lim \left( {\frac{{3n - 1}}{{n{{.2}^n}}} + 2024} \right)\).
Cho dãy số (un) xác định bởi \(\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = {u_n} + 3,\forall n \in \mathbb{N}*\end{array} \right.\). Tính \(\lim \frac{{{u_n}}}{{5n + 2024}}\).
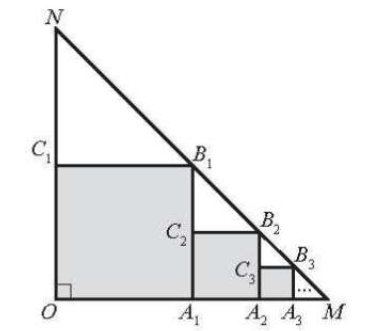
Cho tam giác OMN vuông cân tại O, OM = ON = 5. Trong tam giác OMN, vẽ hình vuông OA1B1C1 sao cho các đỉnh A1; B1; C1 lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác A1MB1, vẽ hình vuông A1A2B2C2 sao cho các đỉnh A2; B2; C2 lần lượt nằm trên các cạnh A1M, MB1, A1B1. Tiếp tục quá trình đó mãi mãi, ta được một dãy các hình vuông (tham khảo hình vẽ dưới đây). Tính tổng diện tích các hình vuông này (làm tròn kết quả đến hàng phần trăm).
Số thập phân vô hạn tuần hoàn 0,511111... viết dạng phân số có dạng \(\frac{a}{b}\) với a; b là các số tự nhiên và \(\frac{a}{b}\) là phân số tối giản. Tính \(\left| {b - 2a} \right|\).
Tìm giới hạn: \(\lim \frac{{\sqrt {9{n^2} + 2n} - 3n}}{{4n + 3}}\).

