20 câu Trắc nghiệm Toán 11 Cánh diều Bài 1. Đường thẳng và mặt phẳng trong không gian (Đúng-sai, trả lời ngắn) có đáp án
20 câu hỏi
Trong các khẳng định sau, khẳng định nào đúng?
Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
6.
4.
3.
2.
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Ba điểm phân biệt.
Một điểm và một đường thẳng.
Hai đường thẳng cắt nhau.
Bốn điểm phân biệt.
Trong các khẳng định sau, khẳng định nào đúng?
Nếu 3 điểm A, B, C là 3 điểm chung của 2 mặt phẳng (P) và (Q) thì A, B, C thẳng hàng.
Nếu A, B, C thẳng hàng và (P), (Q) có điểm chung là A thì B, C cũng là 2 điểm chung của (P) và (Q).
Nếu 3 điểm A, B, C là 3 điểm chung của 2 mặt phẳng (P) và (Q) phân biệt thì A, B, C không thẳng hàng.
Nếu A, B, C thẳng hàng và A, B là 2 điểm chung của (P) và (Q) thì C cũng là điểm chung của (P) và (Q).
Trong các mệnh đề sau đây, mệnh đề nào sai?
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng phân biệt thì có một điểm chung thì chúng có một đường thẳng chung duy nhất.
Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau.
Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB // CD). Khẳng định nào sau đây là sai?
Hình chóp S.ABCD có 4 mặt bên.
Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).
Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC).
Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của BCD.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, giao điểm của BD và AC là O. Gọi M là trung điểm của SC. Gọi I là giao điểm của AM với mặt phẳng (SBD). Mệnh đề nào dưới đây sai?
I SO.
I SC.
I (SBD).
I (SAC).
Cho tứ diện \(ABCD\). \(G\) là trọng tâm của tam giác \(BCD\). Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\) là:
\(AM\) (\(M\) là trung điểm của \(AB\)).
\(AN\) (\(N\) là trung điểm của \(CD\)).
\(AH\) (\(H\) là hình chiếu của \(B\) trên \(CD\)).
\(AK\) (\(K\) là hình chiếu của \(C\) trên \(BD\)).
Cho tứ diện \(ABCD\). Gọi \(M,N\) lần lượt là trung điểm \(AB\) và \(CD\). Mặt phẳng \[(\alpha )\] đi qua \(MN\), cắt \(AD\), \(BC\) lần lượt tại \(P\) và \(Q\). Biết \(MP\) cắt \(NQ\) tại \(I\). Ba điểm nào sau đây thẳng hàng?
\(I,A,C\).
\(I,B,D\).
\(I,A,B\).
\(I,D,C\).
Cho tứ diện ABCD. Gọi G là trọng tâm BCD, M là trung điểm CD, I là điểm ở trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
AM = (ACD) (ABG).
A, J, M thẳng hàng.
J là trung điểm của AM.
DJ = (ACD) (BDJ).
Cho hình chóp S.ABCD có AD cắt BC tại E. Lấy M thuộc cạnh SB và O là giao điểm AC với BD. Khi đó
a) (SAD) (SBC) = SE.
b) Giao tuyến của hai mặt phẳng (MAD) và (SBD) là đường thẳng MD.
c) Gọi I = SO DM. Gọi N là giao điểm giữa đường thẳng SC và mặt phẳng (MAD). Khi đó ba điểm A, I, N thẳng hàng.
d) Gọi N là giao điểm giữa đường thẳng SC và mặt phẳng (MAD). Khi đó N AM.
Cho tứ giác ABCD có AC và BD giao nhau tại O và một điểm S không thuộc mặt phẳng (ABCD). Trên đoạn SC lấy một điểm M không trùng với S và C, K = AM SO. Khi đó:
a) SO là giao tuyến của hai mặt phẳng (SAC) và (ABC).
b) SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
c) Giao điểm của đường thẳng SO với mặt phẳng (ABM) là điểm K.
d) Giao điểm của đường thẳng SD với mặt phẳng (ABM) là điểm N thuộc đường thẳng AK.
Cho hình chóp tứ giác S.ABCD có E là một điểm thuộc miền trong của tam giác SCD như hình vẽ. Gọi F là giao điểm của BE với mặt phẳng (SAC) và G là giao điểm của SC với mặt phẳng (ABE).
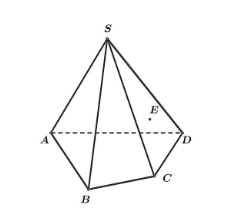
a) (SBE) (ABCD) = BH với H là giao điểm của SE và CD.
b) Đường thẳng SF nằm trong mặt phẳng (SAE).
c) Hai đường thẳng SC và AF cắt nhau tại G.
d) Ba điểm E, G, K thẳng hàng với K là giao điểm của AB và CD.
Cho hình chóp \(S.ABCD\) với \(M\) là một điểm trên cạnh \(SC,N\) là một điểm trên cạnh \(BC\). Gọi \(O = AC \cap BD\) và \(K = AN \cap CD\). Khi đó:
a) \(SO\) là giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\).
b) Giao điểm của đường thẳng \(AM\) và mặt phẳng \((SBD)\) là điểm nằm trên cạnh \(SO\).
c) \(KM\) là giao tuyến của hai mặt phẳng \((AMN)\) và \((SCD)\).
d) Giao điểm của đường thẳng \(SD\) và mặt phẳng \((AMN)\) là điểm nằm trên cạnh \(KM\).
Trong mặt phẳng (α) cho tứ giác ABCD, điểm E (α). Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong năm điểm A, B, C, D, E.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. M là trung điểm của SC, N là trung điểm của OB. Gọi E là giao điểm của đường thẳng SD và mặt phẳng (AMN). Tỉ số \(\frac{{SE}}{{SD}}\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I là điểm nằm trên cạnh AB thỏa mãn \(BI = \frac{1}{3}BA\). Gọi E là giao điểm của BC và mặt phẳng (SDI). Tỉ số \(\frac{{EB}}{{EC}}\) bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của AB, AD và G là trung điểm SO. Mặt phẳng (MNG) cắt SC tại điểm H. Tính \(\frac{{SH}}{{SC}}\).
Hình chóp có 16 cạnh thì có bao nhiêu mặt?
Cho hình bình hành \(ABCD\) và một điểm \(S\) không thuộc mặt phẳng \((ABCD)\), các điểm \(M,N\) lần lượt là trung điểm của đoạn thẳng \(AB,SC\). Gọi \(O = AC \cap BD\).
a) \(SO\) giao tuyến của hai mặt phẳng \((SAC)\) và \((SBD)\).
b) Giao điểm của \(I\) của đường thẳng \(AN\) và mặt phẳng \((SBD)\) là điểm nằm trên đường thẳng \(SO\).
c) Giao điểm của \(J\) của đường thẳng \(MN\) và mặt phẳng \((SBD)\) là điểm nằm trên đường thẳng \(SD\).
d) Ba điểm \(I,J,B\) thẳng hàng.
