20 câu trắc nghiệm Toán 10 Chân trời sáng tạo Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
Từ mẫu số liệu về số quần áo bán được của 23 cửa hàng tại một thành phố trong một tháng, người ta tính được tứ phân vị của mẫu số liệu là 
. Tìm khoảng tứ phân vị của mẫu số liệu trên.
A. 
.
.
C. 
.
D. 
.
Hãy tìm khoảng biến thiên của mẫu số liệu thống kê sau:
.
B. 
.
C. 
.
D. 
.
Mẫu số liệu sau cho biết số ghế trống tại một rạp chiếu phim trong 9 ngày:
7822201518191311.
Khoảng tứ phân vị cho mẫu số liệu là
.
B. 
.
C. 
.
D. 
.
Theo kết quả thống kê điểm thi học kỳ 1 môn toán khối 10 của một trường THPT, người ta tính được phương sai của bảng thống kê đó là 
. Độ lệch chuẩn của bảng thống kê đó gần nhất với số nào sau đây?
A. 
.
.
C. 
.
D. 
.
Điểm kiểm tra môn Toán của 20 học sinh được cho bởi bảng sau:
Trong mẫu số liệu trên có bao nhiêu giá trị bất thường?
.
B. 
.
C. 
.
D. 
.
Chỉ số IQ và EQ tương ứng của một nhóm học sinh được đo và ghi lại ở bảng sau:
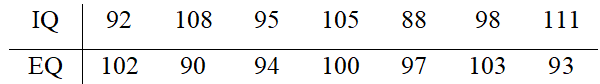
Dựa vào khoảng biến thiên của hai mẫu số liệu “IQ” và “EQ”, hãy chỉ ra mẫu số liệu nào có độ phân tán lớn hơn.
Mẫu số liệu “IQ” có độ phân tán lớn hơn mẫu số liệu “EQ”.
Mẫu số liệu “EQ” có độ phân tán lớn hơn mẫu số liệu “IQ”.
Hai mẫu số liệu có độ phân tán bằng nhau.
Tất cả đều sai.
Sĩ số học sinh của 5 lớp khối 10 là: 40; 43; 45; 41; 46. Độ lệch chuẩn của mẫu số liệu trên gần nhất với số nào trong các đáp án sau?
A. 
.
.
C. 
.
D. 
.
Độ tuổi của 11 cầu thủ ở đội hình xuất phát của một đội bóng đá được ghi lại ở bảng sau:
Giá trị bất thường trong mỗi mẫu số liệu trên là:
Không có giá trị bất thường.
Điểm thi môn Toán lớp 10A của một Trường trung học phổ thông được trình bày ở bảng phân bố tần số sau:
Điểm thi |
|
|
|
|
|
|
|
Tần số |
|
|
|
|
|
|
|
Trong các giá trị dưới đây, giá trị nào gần nhất với phương sai của bảng phân bố tần số trên?
A. 
.
B. 
.
C. 
.
.
Điều tra 
hộ dân cư để xem xét mức tiêu dùng nước sạch bình quân theo đầu người trong một tháng người ta thu được số liệu sau:
Chọn phát biểu sai.
Mức tiêu thụ trung bình ở Thành phố A là 
/ người.
Mức tiêu thụ trung bình ở Thành phố B là 
/ người.
Phương sai của mức tiêu thụ ở Thành phố A cao hơn ở Thành phố B.
Độ lệch chuẩn của mức tiêu thụ ở Thành phố A thấp hơn ở Thành phố B.
Phần II. Trắc nghiệm đúng, sai
a) Điểm thấp nhất của xạ thủ A là 6.
b) Điểm trung bình của xạ thủ A cao hơn điểm trung bình của xạ thủ B.
c) Độ lệch chuẩn bảng điểm của xạ thủ A lớn hơn độ lệch chuẩn bảng điểm của xạ thủ B.
d) Xạ thủ A bắn đều hơn xạ thủ B
a) Khoảng biến thiên của mẫu số liệu là 50.
b) Giá trị trung bình của mẫu số liệu là 97,5.
c) Khoảng tứ phân vị của mẫu số liệu là 
.
d) Mẫu số liệu không có giá trị bất thường
a) Khoảng biến thiên của mẫu số liệu điểm kiểm tra của An là 
.
b) Điểm kiểm tra trung bình của học sinh An là 
.
c) Điểm kiểm tra trung bình của học sinh Bình là 
d) Bạn An học đều hơn bạn Bình.
a) Kích thước mẫu trong bảng số liệu là 25
b) Độ chênh lệch giữa giá trị trung bình và trung vị của bảng số liệu lớn hơn 1.
c) Tứ phân vị thứ ba của bảng số liệu là 
.
d) Bảng số liệu có giá trị bất thường là 4 và 10
a) Số bàn thắng trung bình của đội tuyển Việt Nam và đội tuyển Thái Lan là không bằng nhau.
b) Xét mẫu số liệu về số bàn thắng của đội tuyển Việt Nam có độ lệch chuẩn là: 
(bàn).
c) Xét mẫu số liệu về số bàn thắng của đội tuyển Thái Lan có phương sai là: 
.
d) Khả năng ghi bàn của đội tuyển Thái Lan có tính ổn định hơn so với đội tuyển Việt Nam.
Cho mẫu số liệu 
. Biết giá trị trung bình của mẫu số liệu 
và độ lệch chuẩn của mẫu số liệu 
. Tính 
.
Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: °C).
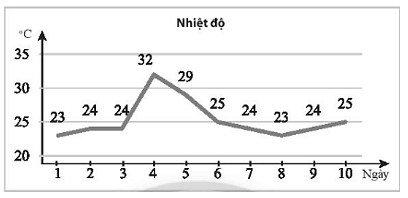
Hãy tìm phương sai của mẫu số liệu đó.
Điểm thi học sinh trong đợt kiểm tra đầu vào môn Tiếng Anh của hai lớp 3A và 3B được xác định bởi bảng sau:
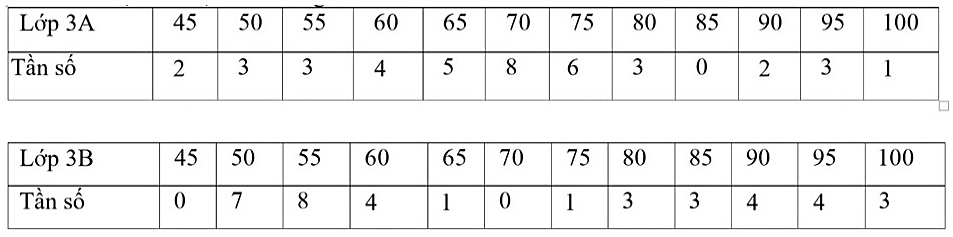
Tính tỉ số phương sai của học sinh 3B với học sinh 3A (làm tròn kết quả đến hàng phần trăm).
Có 100 học sinh tham dự kì thi học sinh giỏi Toán. Kết quả cho trong bảng sau:
Tính độ lệch chuẩn của mẫu số liệu trên (làm tròn kết quả đến hàng phần trăm).
Mẫu số liệu sau cho biết số giờ nghỉ của từng tháng, trong 9 tháng của anh Nam như sau:
Tìm khoảng tứ phân vị cho mẫu số liệu này.
