20 câu trắc nghiệm Toán 10 Chân trời sáng tạo Bài 3. Tích của một số với một vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Cho \(\overrightarrow a \ne \overrightarrow 0 \) và điểm \(O\). Gọi \(M,N\) lần lượt là hai điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow a \) và \(\overrightarrow {ON} = - 4\overrightarrow a \). Khi đó:
\(\overrightarrow {MN} = 7\overrightarrow a \).
\(\overrightarrow {MN} = - 5\overrightarrow a \).
\(\overrightarrow {MN} = - 7\overrightarrow a \).
\(\overrightarrow {MN} = - 5\overrightarrow a \).
Cho tam giác \(ABC\). Gọi \(I\) là trung điểm của \(AB\). Tìm điểm \(M\) thỏa mãn hệ thức \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
\(M\) là trung điểm của \(BC\).
\(M\)là trung điểm của \(IC\).
\(M\) là trung điểm của \(IA\).
\(M\) là điểm trên cạnh \(IC\) sao cho \(IM = 2MC\).
Cho \(\Delta ABC\) và một điểm M tùy ý. Chọn hệ thức đúng?
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = \overrightarrow {AC} + 2\overrightarrow {BC} \).
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {AC} + \overrightarrow {BC} \).
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {CA} + \overrightarrow {CB} \).
\(2\overrightarrow {MA} + \overrightarrow {MB} - 3\overrightarrow {MC} = 2\overrightarrow {CB} - \overrightarrow {CA} \).
Cho tam giác \(ABC\). Gọi \(M\) là trung điểm của \(BC\) và \(N\) là trung điểm \(AM\). Đường thẳng \(BN\) cắt \(AC\) tại \(P\). Khi đó \(\overrightarrow {AC} = x\overrightarrow {CP} \) thì giá trị của \(x\) là:
\( - \frac{4}{3}\).
\( - \frac{2}{3}\).
\( - \frac{3}{2}\).
\( - \frac{5}{3}\).
Cho \(\Delta ABC\). Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Phân tích \(\overrightarrow {AB} \) theo hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {CP} \) ta được
\(\overrightarrow {AB} = \frac{4}{3}\overrightarrow {BN} - \frac{2}{3}\overrightarrow {CP} \).
\(\overrightarrow {AB} = - \frac{4}{3}\overrightarrow {BN} + \frac{2}{3}\overrightarrow {CP} \).
\(\overrightarrow {AB} = - \frac{4}{3}\overrightarrow {BN} - \frac{2}{3}\overrightarrow {CP} \).
\(\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {BN} - \frac{4}{3}\overrightarrow {CP} \).
Cho hình bình hành ABCD có E, N lần lượt là trung điểm của BC, AE. Tìm các số p và q sao cho \(\overrightarrow {DN} = p\overrightarrow {AB} + q\overrightarrow {AC} \).
\(p = \frac{5}{4};q = \frac{3}{4}\).
\(p = - \frac{4}{3};q = \frac{2}{3}\).
\(p = - \frac{4}{3};q = - \frac{2}{3}\).
\(p = \frac{5}{4};q = - \frac{3}{4}\).
Cho tam giác \(ABC\) với phân giác trong \(AD\). Biết \(AB = 5\), \(BC = 6\), \(CA = 7\). Khi đó \(\overrightarrow {AD} \) bằng
\(\frac{5}{{12}}\overrightarrow {AB} + \frac{7}{{12}}\overrightarrow {AC} \).
\(\frac{7}{{12}}\overrightarrow {AB} - \frac{5}{{12}}\overrightarrow {AC} \).
\(\frac{7}{{12}}\overrightarrow {AB} + \frac{5}{{12}}\overrightarrow {AC} \).
\(\frac{5}{{12}}\overrightarrow {AB} - \frac{7}{{12}}\overrightarrow {AC} \).
Cho \(\Delta ABC\) có trọng tâm G, điểm M thỏa mãn \(2\overrightarrow {MA} + \overrightarrow {MB} + 3\overrightarrow {MC} = \overrightarrow 0 \). Khi đó điểm M thỏa mãn hệ thức nào sau đây?
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {BC} \).
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {CA} \).
\(\overrightarrow {GM} = \frac{1}{6}\overrightarrow {AB} \).
\(\overrightarrow {GM} = \frac{1}{3}\overrightarrow {CB} \).
Gọi G là trọng tâm của \(\Delta ABC\). Tập hợp điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 6\) là:
Đường tròn ngoại tiếp tam giác ABC.
Đường tròn tâm G bán kính là 1.
Đường tròn tâm G bán kính là 2.
Đường tròn tâm G bán kính là 6.
Cho \(\Delta ABC,E\) là trung điểm BC, I là trung điểm của AB. Gọi D, I, J, K lần lượt là các điểm thỏa mãn \(\overrightarrow {BE} = 2\overrightarrow {BD} ,\overrightarrow {AJ} = \frac{1}{2}\overrightarrow {JC} ,\overrightarrow {IK} = m\overrightarrow {IJ} \). Tìm m để A, K, D thẳng hàng.
\(m = \frac{5}{6}\).
\(m = \frac{1}{3}\).
\(m = \frac{1}{2}\).
\(m = \frac{2}{5}\).
Phần II. Trắc nghiệm đúng, sai
Cho bốn điểm \(A,B,C,D\) có \(M,N\) là trung điểm của \(AB,CD\).
a) \(\overrightarrow {MA} + \overrightarrow {MB} = \vec 0\).
b) \(\overrightarrow {NC} + \overrightarrow {ND} = \vec 0{\rm{. }}\)
c) \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} \).
d) \(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} {\rm{. }}\)
Gọi \[AN,{\rm{ }}CM\] là các đường trung tuyến của tam giác \[ABC\] và G là trọng tâm.
a) \[\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AC} \,.\]
b) \[\overrightarrow {CM} = \frac{3}{2}\overrightarrow {GC} \,.\]
c) \[\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {BC} - \overrightarrow {BA} } \right)\,.\]
d) \[\overrightarrow {AB} = \frac{4}{3}\overrightarrow {AN} + \frac{2}{3}\overrightarrow {CM} \].
Cho hình bình hành \(ABCD\) và các điểm \(M,N,P\) thoả mãn \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} \), \(\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AC} ,\) \(\overrightarrow {AP} = \frac{1}{4}\overrightarrow {AD} \).
a) \(\overrightarrow {AN} = \frac{1}{6}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\).
b) \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AD} .\)
c) \(\overrightarrow {MP} = \frac{1}{3}\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AB} \).
d) Ba điểm \(M,N,P\) thẳng hàng.
Cho hình vuông \(ABCD\) tâm \(O\) cạnh \(a\). \(G\) là trọng tâm tam giác \(ABC\).
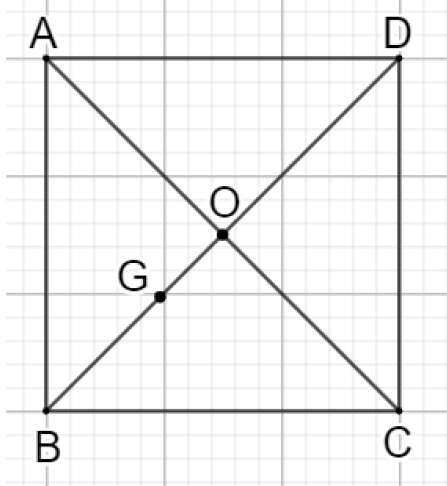
a) \(\overrightarrow {AC} = - 2\overrightarrow {AO} \).
b) \(\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \).
c) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
d) \(\left| {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right| = 2a\).
Cho \(\Delta ABC\) nội tiếp đường tròn tâm \(O,H\) là trực tâm tam giác, \(D\) là điểm đối xứng của \(A\) qua \(O\).
a) \(BD{\rm{//}}CH\).
b) \(CD{\rm{//}}BH\).
a) \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 3\overrightarrow {HO} \).
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OH} \).
Phần III. Trắc nghiệm trả lời ngắn
Cho \(\Delta ABC\) vuông tại \(B\) có \(\widehat A = 30^\circ ,AB = a\). Gọi \(I\) là trung điểm của \(AC\). Khi đó, ta tính được \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng \(\frac{{a\sqrt m }}{3}\). Xác định m.
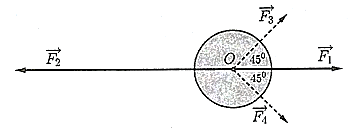
Một vật đang ở vị trí \(O\) chịu hai lực tác dụng ngược chiều nhau là \({\vec F_1}\) và \(\overrightarrow {{F_2}} \), trong đó độ lớn lực \({\vec F_2}\) lớn gấp đôi độ lớn lực \({\vec F_1}\). Người ta muốn vật dừng lại nên cần tác dụng vào vật hai lực \({\vec F_3},{\vec F_4}\) có phương hợp với lực \({\vec F_1}\) các góc \(45^\circ \) như hình vẽ, chúng có độ lớn bằng nhau và bằng \(20\;{\rm{N}}\). Hỏi độ lớn của lực \(\overrightarrow {{F_2}} \) bằng bao nhiêu Newton (làm tròn kết quả đến hàng phần mười)?
Cho hình bình hành \(ABCD\) tâm \(O\). Lấy các điểm \(I\), \(J\) sao cho \(3\overrightarrow {IA} + 2\overrightarrow {IC} - 2\overrightarrow {ID} = \vec 0;\) \(\overrightarrow {JA} - 2\overrightarrow {JB} + 2\overrightarrow {JC} = \vec 0\). Khi đó \(\overrightarrow {IJ} = k\overrightarrow {IO} \), vậy \(k = ?\)
Cho hình bình hành \(ABCD\) tâm \(O\). Lấy các điểm \(I\), \(J\) sao cho \(3\overrightarrow {IA} + 2\overrightarrow {IC} - 2\overrightarrow {ID} = \vec 0;\)\(\overrightarrow {JA} - 2\overrightarrow {JB} + 2\overrightarrow {JC} = \vec 0\). Khi đó \(\overrightarrow {IJ} = k\overrightarrow {IO} \), vậy \(k = ?\)
Cho tứ giác \(ABCD\). Gọi \(I,J\) theo thứ tự là trung điểm của \(AB,CD\) và \(IJ = \frac{5}{4}\). Gọi \(M,N\) theo thứ tự là trung điểm của \(BC,AC\). Tính \(\left| {\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CI} } \right|\).




