20 câu trắc nghiệm Toán 10 Chân trời sáng tạo Bài 2: Hệ bất phương trình bậc nhất hai ẩn (Đúng sai - Trả lời ngắn) có đáp án
35 câu hỏi
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình\[\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.\]?
\[\left( { - 1;4} \right)\].
\[\left( { - 2;4} \right)\].
\[\left( {0;0} \right)\].
\[\left( { - 3;4} \right)\].
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{2x - 5y - 1 > 0}\\{2x + y + 5 > 0}\\{x + y + 1 < 0}\end{array}} \right.\]?
\[\left( {0;0} \right)\]
\[\left( {1;0} \right)\].
\[\left( {0; - 2} \right)\].
\[\left( {0;2} \right)\].
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y > 0\\2x + 5y < 0\end{array} \right.\) có tập nghiệm là \(S\). Khẳng định nào sau đây là khẳng định đúng?
\(\left( {1;1} \right) \in S\).
\(\left( { - 1; - 1} \right) \in S\).
\(\left( {1; - \frac{1}{2}} \right) \in S\).
\(\left( { - \frac{1}{2};\frac{2}{5}} \right) \in S\).
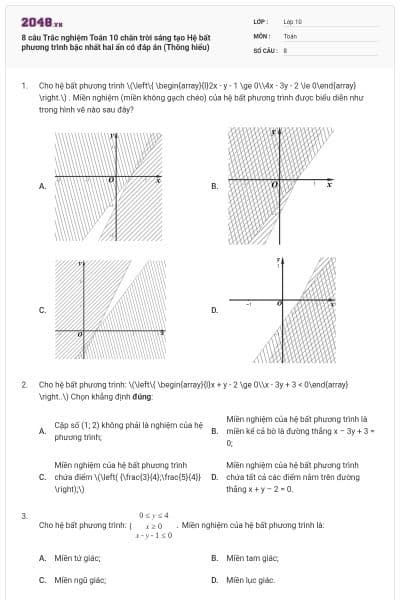
Miền tam giác \[ABC\] kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
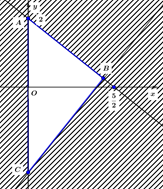
Cho hệ . Gọi \({S_1}\) là tập nghiệm của bất phương trình (1), \({S_2}\) là tập nghiệm của bất phương trình (2) và \(S\) là tập nghiệm của hệ thì
\({S_1} \subset {S_2}\).
\({S_2} \subset {S_1}\).
\({S_2} = S\).
\({S_1} \ne S\).
Phần không tô màu là hình biểu diễn miền nghiệm của hệ bất phương trình nào?
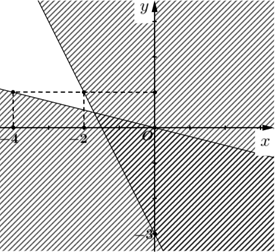
\(\left\{ \begin{array}{l}x + 4y > 0\\2x + y + 3 > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y < 0\\2x + y + 3 \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y > 0\\2x + y + 3 \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + 4y \ge 0\\2x + y + 3 \ge 0\end{array} \right.\).
Giá trị nhỏ nhất của biểu thức trên miền xác định bởi hệ là\(F = y - x\)
\(\min F = 1\) khi \(x = 2\), \(y = 3\).
\(\min F = 2\) khi \(x = 0\), \(y = 2\).
\(\min F = 3\) khi \(x = 1\), \(y = 4\).
\(\min F = 0\) khi \(x = 0\), \(y = 0\).
Cho hệ bất phương trình . Khẳng định nào sau đây là khẳng định sai?
Trên mặt phẳng tọa độ \(Oxy\), biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác \(ABCO\) kể cả các cạnh với \(A\left( {0;3} \right)\), \(B\left( {\frac{{25}}{8};\frac{9}{8}} \right)\), \(C\left( {2;0} \right)\) và \(O\left( {0;0} \right)\).
Đường thẳng \(\Delta :x + y = m\) có giao điểm với tứ giác \(ABCO\) kể cả khi \( - 1 \le m \le \frac{{17}}{4}\).
Giá trị lớn nhất của biểu thức \(x + y\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình đã cho là \(\frac{{17}}{4}\).
Giá trị nhỏ nhất của biểu thức \(x + y\), với \(x\) và \(y\) thỏa mãn hệ bất phương trình đã cho là 0.
Giá trị lớn nhất của biết thức F(x,y) = x + 2y với điều kiện là
\[6\].
\[8\].
\[10\].
\[12\].
Biểu thức \[F = y--x\] đạt giá trị nhỏ nhất với điều kiện \[\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \le - 2}\\{x - 2y \le 2}\\{x + y \le 5}\\{x \ge 0}\end{array}} \right.\]tại điểm \[S\left( {x;y} \right)\] có toạ độ là
\[\left( {4;1} \right)\].
\[\left( {3;1} \right)\].
\[\left( {2;1} \right)\].
\[\left( {1;1} \right)\].
a) Hệ trên là một hệ bất phương trình bậc nhất hai ẩn.
b) \(\left( { - 2;8} \right)\) là một nghiệm của hệ bất phương trình trên.
c) \(\left( {3\,;1} \right)\) là một nghiệm của hệ bất phương trình trên.
d) \(\left( { - 2; - 1} \right)\) là một nghiệm của hệ bất phương trình trên.
a) Gọi \(x,y\) (đơn vị: triệu đồng) tiền bác Linh đầu tư vào khoản \(X\) và khoản Y, ta có hệ bất phương trình:\(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y}\end{array}} \right.\).
b) Miền nghiệm của hệ bất phương trình tiền bác Linh đầu tư là một tứ giác.
c) Điểm \(C\left( {200\,;\,40} \right)\) không thuộc miền nghiệm của hệ bất phương trình tiền bác Linh đầu tư.
d) Điểm \(A\left( {180\,;\,60} \right)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Linh đầu tư.
a) Hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}26x + 22y \ge 56\\26x + 22y \le 91\\x \le y\\x \ge 0\\y \ge 0\end{array}\end{array}} \right.\).
b) Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là một ngũ giác.
c) \(\left( {1;2} \right)\) thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông.
d) Điểm \(B\left( {\frac{{91}}{{48}};\frac{{91}}{{48}}} \right)\) là điểm có hoành độ bé nhất thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông.
a) Hệ bất phương mô tả số gói thực phẩm \(X\) và thực phẩm \(Y\) mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin \(B\) là \(\left\{ {\begin{array}{*{20}{l}}{x + y \ge 12}\\{2x + y \ge 16}\\{x + 2y \ge 14}\\{0 \le x \le 12}\\{0 \le y \le 12}\end{array}} \right.\).
b) Miền nghiệm của hệ bất phương mô tả số gói thực phẩm \(X\) và thực phẩm \(Y\) mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin \(B\)là một ngũ giác.
c) Biết 1 gói thực phẩm loại \(X\) giá 20000 đồng, 1 gói thực phẩm loại \(Y\) giá 25000 đồng. Bà Lan cần dùng 10 gói thực phẩm loại \(X\) và 2 gói thực phẩm loại \(Y\) để chi phí mua là ít nhất.
d) Điểm \(\left( {10;8} \right)\) không thuộc miền nghiệm của hệ bất phương mô tả số gói thực phẩm \(X\) và thực phẩm \(Y\) mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin \(B\).
a) Gọi \(x,y\) (xe) lần lượt là số xe loại A và B cần thuê. Khi đó, số tiền cần bỏ ra để thuê xe là \(F\left( {x;y} \right) = 5x + 4y\) (triệu đồng).
b) Gọi \(x,y\) (xe) lần lượt là số xe loại A và B cần thuê, ta có hệ bất phương trình biểu thị các điều kiện của bài toán là: \(\left\{ \begin{array}{l}30x + 20y \ge 180\\0,8x + 1,6y \ge 8\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\left( * \right).\)
c) Điểm \(M\left( {4\,;2} \right)\) thuộc miền nghiệm của hệ bất phương trình biểu thị các điều kiện của bài toán.
d) Công ty cần thuê 4 xe loại \(A\) và 3 xe loại \(B\) thì chi phí thấp nhất.
Phần III. Trắc nghiệm trả lời ngắn
Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm \(I\) và \(II\). Mỗi sản phẩm \(I\) bán lãi \(500\) nghìn đồng, mỗi sản phẩm \(II\) bán lãi \(400\) nghìn đồng. Để sản xuất được một sản phẩm \(I\) thì Chiến phải làm việc trong \(3\) giờ, Bình phải làm việc trong \(1\) giờ. Để sản xuất được một sản phẩm \(II\) thì Chiến phải làm việc trong \(2\) giờ, Bình phải làm việc trong \(6\) giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá \(180\) giờ và Bình không thể làm việc quá \(220\) giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là bao nhiêu triệu đồng?
Trong một cuộc thi pha chế, hai đội A, B được sử dụng tối đa \(24g\) hương liệu, \(9\) lít nước và \(210\)g đường để pha chế nước cam và nước táo. Để pha chế \(1\) lít nước cam cần \(30\)g đường, \(1\) lít nước và \(1\)g hương liệu; pha chế \(1\) lít nước táo cần \(10\)g đường, \(1\) lít nước và \(4\)g hương liệu. Mỗi lít nước cam nhận được \(60\) điểm thưởng, mỗi lít nước táo nhận được \(80\) điểm thưởng. Đội A pha chế được \(a\) lít nước cam và \(b\) lít nước táo và dành được điểm thưởng cao nhất. Tính hiệu số \(a - b\).
Có ba nhóm máy \[A,B,C\] dùng để sản xuất ra hai loại sản phẩm \[I\] và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
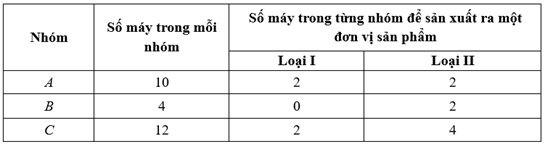
Một đơn vị sản phẩm loại \[I\] lãi ba triệu đồng, một đơn vị sản phẩm loại \[II\] lãi năm triệu đồng. Hỏi lợi nhuận cao nhất mà đơn vị thu được là bao nhiêu? (Đơn vị là triệu đồng).
Một nhà nông dân nọ có 8 sào đất trồng hoa màu. Biết rằng 1 sào trồng Đậu cần 20 công và lãi được 3 triệu đồng, 1 sào trồng Cà cần 30 công và lãi được 4 triệu đồng. Người nông dân trồng được x sào Đậu và y sào Cà thì thu được tiền lãi cao nhất. Tính giá trị biểu thức \(F = 3x + 2y\) biết rằng tổng số công không quá 180.
Trường THPT X tổ chức gian hàng Hội Xuân, lớp 10C lên kế hoạch bán trà sữa và bánh flan để vui và kiếm lời, toàn bộ số tiền lời thu được sẽ quyên góp để gây quỹ khuyến học cho các bạn khó khăn trong trường. Lớp có số tiền vốn là 630 nghìn đồng, biết một ly trà sữa kèm topping có giá vốn là \(15\) nghìn đồng, bán ra lãi \(5\) nghìn đồng; một cái bánh flan có giá vốn là \(3\) nghìn đồng, bán ra lãi \(2\) nghìn đồng. Để được giá sỉ thì lớp phải nhập từ \(20\) ly trà sữa và từ \(20\) cái bánh flan trở lên, theo khảo sát nhu cầu thì không thể bán vượt quá \(40\) cái bán flan. Lớp 10C cần tính toán số lượng ly trà sữa và bánh flan để thu được lợi nhuận lớn nhất, khi đó lợi nhuận lớn nhất là bao nhiêu? (đơn vị tính: nghìn đồng).